题目内容
已知m,n,m+n成等差数列,m,n,mn成等比数列,则椭圆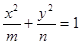 的离心率为_______________
的离心率为_______________
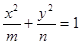 的离心率为_______________
的离心率为_______________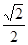
由等差中项与等比中项,列方程组可解得m,n的值,再求椭圆的离心率即可.
解答:解: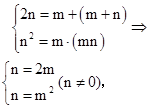
∴m2=2m,又m≠0,得m=2,n=4
∴椭圆为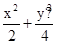 =1,
=1,
c2=4-2=2,得c=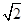 ,又a=2,
,又a=2,
∴e=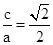 .
.
故答案为: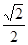 .
.
解答:解:
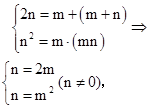
∴m2=2m,又m≠0,得m=2,n=4
∴椭圆为
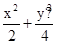 =1,
=1,c2=4-2=2,得c=
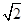 ,又a=2,
,又a=2,∴e=
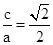 .
.故答案为:
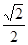 .
.
练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
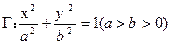 的左、右焦点为
的左、右焦点为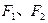 ,过点
,过点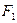 斜率为正数的直线交
斜率为正数的直线交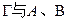 两点,且
两点,且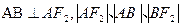 成等差数列。
成等差数列。 的离心率;
的离心率;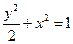 ,斜率为
,斜率为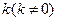 的直线
的直线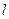 过椭圆的上焦点且与椭圆相交于
过椭圆的上焦点且与椭圆相交于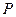 ,
,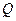 两点,线段
两点,线段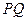 的垂直平分线与
的垂直平分线与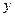 轴相交于点
轴相交于点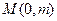 .
.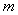 的取值范围;
的取值范围; 面积的最大值.
面积的最大值.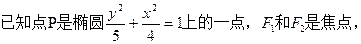
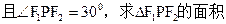
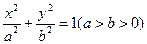 的左焦点为
的左焦点为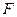 (-1,0),离心率为
(-1,0),离心率为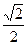 ,过点
,过点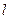 与椭圆C交于
与椭圆C交于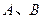 两点.
两点.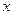 轴交于点G,求点G横坐标的取值范围.
轴交于点G,求点G横坐标的取值范围.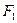 、
、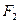 分别是椭圆
分别是椭圆 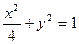 的左、右焦点,
的左、右焦点,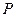 是该椭圆上的一个动点,
是该椭圆上的一个动点,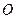 为坐标原点.
为坐标原点. 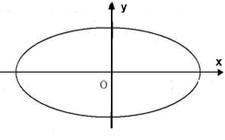
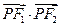 的取值范围;
的取值范围; 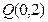 的直线
的直线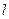 与椭圆交于不同的两点M、N,且∠
与椭圆交于不同的两点M、N,且∠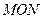 为锐角,求直线
为锐角,求直线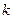 的取值范围
的取值范围 .
.

 已知A(-2,0),B(2,0)为椭圆C的左、右顶点,F为其右焦点,P是椭圆C上异于A、B的动点,且
已知A(-2,0),B(2,0)为椭圆C的左、右顶点,F为其右焦点,P是椭圆C上异于A、B的动点,且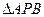 面积的最大值为
面积的最大值为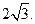
 转动时,试判断以BD为直径的圆与直线PF的位置关系,并加以证明。
转动时,试判断以BD为直径的圆与直线PF的位置关系,并加以证明。 ,
, 的离心率为
的离心率为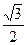 ,过其右焦点斜率为
,过其右焦点斜率为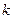 (
( )的直线与椭圆交于A,B两点,若
)的直线与椭圆交于A,B两点,若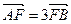 ,则
,则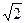 C
C  D 2
D 2