题目内容
甲乙两人各有 个材质、大小、形状完全相同的小球,甲的小球上面标有
个材质、大小、形状完全相同的小球,甲的小球上面标有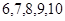 五个数字,乙的小球上面标有
五个数字,乙的小球上面标有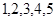 五个数字.把各自的小球放入两个不透明的口袋中,两人同时从各自的口袋中随机摸出
五个数字.把各自的小球放入两个不透明的口袋中,两人同时从各自的口袋中随机摸出 个小球.规定:若甲摸出的小球上的数字是乙摸出的小球上的数字的整数倍,则甲获胜,否则乙获胜.
个小球.规定:若甲摸出的小球上的数字是乙摸出的小球上的数字的整数倍,则甲获胜,否则乙获胜.
(1)写出基本事件空间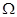 ;
;
(2)你认为“规定”对甲、乙二人公平吗?说出你的理由.
(1)基本事件空间: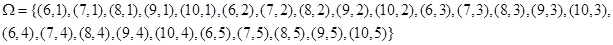
(2)规定是不公平的(理由见解析).
解析试题分析:(1)由题意易求得基本事件空间 .
.
(2)分别求出甲、乙各自获胜的概率,若概率相等,则“规定”对甲乙二人公平;若概率不相等,则“规定”对甲乙二人不公平.
试题解析:(1)用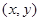 表示发生的事件,其中甲摸出的小球上的数字为
表示发生的事件,其中甲摸出的小球上的数字为 ,乙摸出的小球上的数字为
,乙摸出的小球上的数字为 .则基本事件空间:
.则基本事件空间: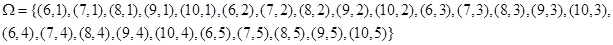
(2)由(1)可知,基本事件总数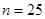 个,设甲获胜的事件为
个,设甲获胜的事件为 ,它包括的基本事件有
,它包括的基本事件有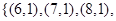
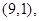
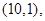
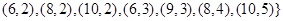 ,共含基本事件个数
,共含基本事件个数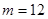 个.
个.
所以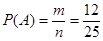 .因此乙获胜的概率为
.因此乙获胜的概率为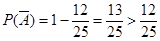 ,即乙获胜的概率大,这个规定是不公平的.
,即乙获胜的概率大,这个规定是不公平的.
考点:随机事件的概率及其应用.

练习册系列答案
相关题目
我国政府对PM2.5采用如下标准:
| PM2.5日均值m(微克/立方米) | 空气质量等级 |
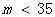 | 一级 |
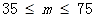 | 二级 |
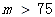 | 超标 |
某市环保局从180天的市区PM2.5监测数据中,随机抽取l0天的数据作为样本,监测值如茎叶图所示(十位为茎,个位为叶).

(1)求这10天数据的中位数.
(2)从这l0天的数据中任取3天的数据,记
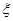 表示空气质量达到一级的天数,求
表示空气质量达到一级的天数,求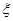 的分布列;
的分布列;(3)以这10天的PM2.5日均值来估计这180天的空气质量情况,其中大约有多少天的空气质量达到一级.
 .已知比赛中,乙先赢了第一局,求:
.已知比赛中,乙先赢了第一局,求: 元的奖金;若中两次奖,则共获得数额为
元的奖金;若中两次奖,则共获得数额为 元的奖金;若中3次奖,则共获得数额为
元的奖金;若中3次奖,则共获得数额为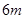 元的奖金。假设顾客每次抽奖中获的概率都是
元的奖金。假设顾客每次抽奖中获的概率都是 ,请问:商场将奖金数额m最高定为多少元,才能使促销方案对商场有利?
,请问:商场将奖金数额m最高定为多少元,才能使促销方案对商场有利?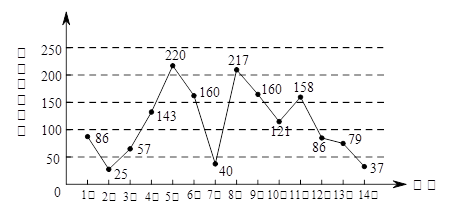
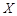 是此人停留期间空气质量优良的天数,请分别求当x=0时,x=1时和x=3时的概率值。
是此人停留期间空气质量优良的天数,请分别求当x=0时,x=1时和x=3时的概率值。
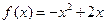 的图象与
的图象与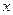 轴围成的区域为M,满足
轴围成的区域为M,满足 的区域为N,若向区域M上随机投一点P,则点P落入区域N的概率为______
的区域为N,若向区域M上随机投一点P,则点P落入区域N的概率为______