��Ŀ����
13����ͼ��һ�����Ϊ1�������Σ��ֽ������²�������һ�β������ֱ�����������������ߵ��е㣬����4�������Σ���ȥ�м�һ�������Σ���ͼ������Ӱ������ʾ����������ȥ�����������������ֱ�ǩ��1�����ڶ��β���������ʣ����������������ߵ��е㣬����ȥ�����м�������Σ���ͼ������Ӱ������ʾ����ͬʱ����ȥ��3���������϶��������ֱ�ǩ��2���������β���������ʣ��ĸ����������ߵ��е㣬����ȥ�����м�������Σ�ͬʱ����ȥ���������϶��������ֱ�ǩ��3�������������ȥ���ǵ�n�β�����ʣ��ͼ�ε������Ϊan��
��1����a1��a2��
��2����ʹʣ��ͼ�ε����������ԭ�����������$\frac{1}{4}$�������پ������ٴβ�����
��3�����n�β�������ȥ��������������������ǩ�ϵ����ֺ�Sn��
���� ��1���۲�ͼ��ֱ�ӿɵý��ۣ�
��2��ͨ��an=${��\frac{3}{4}��^n}��\frac{1}{4}$�����㼴�ý��ۣ�
��3��ͨ�����n�β�����ȥbn�������ο�֪${b_n}={3^{n-1}}$�����ô�λ��������㼴�ý��ۣ�
��� �⣺��1��${a_1}=\frac{3}{4}$��${a_2}=\frac{9}{16}$������4�֣���ÿ��2�֣�
��2����Ϊ{an}����$\frac{3}{4}$Ϊ�����$\frac{3}{4}$Ϊ���ȵĵȱ����У�
����an=${��\frac{3}{4}��^n}$����6�֣�
��${��\frac{3}{4}��^n}��\frac{1}{4}$����3n��4n-1����7�֣�
��Ϊ31��40��32��41��33��42��34��43��35��44��
���Ե�n=5ʱ��${��\frac{3}{4}��^n}��\frac{1}{4}$����8�֣�
�������پ���5�β�������ʹʣ��ͼ�ε����������ԭ�����������$\frac{1}{4}$����9�֣�
��3�����n�β�����ȥbn�������Σ�
��{bn}����1Ϊ���3Ϊ���ȵĵȱ����У�
��${b_n}={3^{n-1}}$����11�֣�
����������������������ǩ�ϵ����ֵĺ�Sn=1��1+2��3+��+n��3n-1����13�֣�
��3Sn=1��3+2��32+��+n��3n��
��ʽ�������-2Sn=��1+3+32+��+3n-1��-n��3n=$\frac{{{3^n}-1}}{2}-n��{3^n}$��
��Sn=$��\frac{n}{2}-\frac{1}{4}����{3^n}+\frac{1}{4}$����14�֣�
���� ������Ҫ����ȱ����С�����ʽ�������ʵȻ���֪ʶ��������ת������ѧ˼�뷽�����Լ���������������������������ע����ⷽ���Ļ��ۣ������е��⣮

| A�� | a��3 | B�� | a��2 | C�� | a��3 | D�� | a��2 |
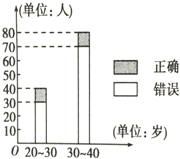 �����Ŵ���ij����̨�Ƴ�����Ϸ��Ŀ��ѡ�����1��8��8�ȴ��ţ����ΰ������ϵ����壬����Ქ��һ�����֣���һ�������и����Ե���ɫ���ɵķ�ʽ�����ѡ������ȷ�ش����������֣����ɻ�ø����Ŷ�Ӧ�ļ�ͥ���������һ�γ�������У����ֲ���ѡ�ֶ�����Ϊ��������Σ�20��30��30��40����λ���꣩����¶Ը�����������������ͼ��ʾ��
�����Ŵ���ij����̨�Ƴ�����Ϸ��Ŀ��ѡ�����1��8��8�ȴ��ţ����ΰ������ϵ����壬����Ქ��һ�����֣���һ�������и����Ե���ɫ���ɵķ�ʽ�����ѡ������ȷ�ش����������֣����ɻ�ø����Ŷ�Ӧ�ļ�ͥ���������һ�γ�������У����ֲ���ѡ�ֶ�����Ϊ��������Σ�20��30��30��40����λ���꣩����¶Ը�����������������ͼ��ʾ������д��2��2���������ж��Ƿ���90%�İ�����Ϊ�¶Ը��������Ƿ��������йأ�˵��������ɣ���������ٽ�ֵ�����ο���
| P��K2��k0�� | 0.10 | 0.05 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 6.635 | 7.879 |
���ο���ʽ��K2=$\frac{{n{{��ad-bc��}^2}}}{��a+b����c+d����a+c����b+d��}$����n=a+b+c+d��
