题目内容
实数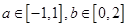 .设函数
.设函数 的两个极值点为
的两个极值点为 ,现向点
,现向点 所在平面区域投掷一个飞镖,则飞镖恰好落入使
所在平面区域投掷一个飞镖,则飞镖恰好落入使 且x2≥1的区域的概率为 ( ▲ ) .
且x2≥1的区域的概率为 ( ▲ ) .
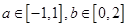 .设函数
.设函数 的两个极值点为
的两个极值点为 ,现向点
,现向点 所在平面区域投掷一个飞镖,则飞镖恰好落入使
所在平面区域投掷一个飞镖,则飞镖恰好落入使 且x2≥1的区域的概率为 ( ▲ ) .
且x2≥1的区域的概率为 ( ▲ ) .A. | B.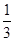 | C.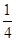 | D.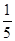 |
C
分析:本题考查的知识点是几何概型的意义,关键是要找出函数f(x)="-"
 x3+
x3+  ax2+bx的两个极值点为x1,x2,使满足x1≤-1且x2≥1的可行域面积的大小和实数a,b满足a∈[-1,1],b∈[0,2]对应的图形面积的大小.
ax2+bx的两个极值点为x1,x2,使满足x1≤-1且x2≥1的可行域面积的大小和实数a,b满足a∈[-1,1],b∈[0,2]对应的图形面积的大小.解:∵f(x)="-"
 x3+
x3+ ax2+bx
ax2+bx
∴f’(x)=-x2+ax+b的两个零点为x1,x2,
∵x1≤-1且x2≥1
∴

在条件实数a∈[-1,1],b∈[0,2]下画出满足上面不等式的图形如右图中阴影部分.
其面积为1,a∈[-1,1],b∈[0,2]围成图形的面积为4
∴现向点(a,b)所在平面区域投掷一个飞镖,则飞镖恰好落入使x1≤-1且x2≥1的区域的概率为
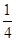
故选C.

练习册系列答案
相关题目
 中,分别以
中,分别以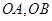 为直径作两个半圆。 在扇形
为直径作两个半圆。 在扇形
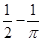
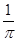


 和
和 ,则( )
,则( ) 内任取一实数
内任取一实数 ,其满足
,其满足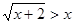 的概率是_________.
的概率是_________. 顶帽子,则恰有1人拿的是自己的帽子的概率 。
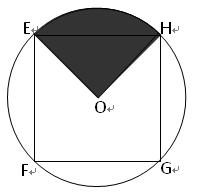
顶帽子,则恰有1人拿的是自己的帽子的概率 。 是以
是以 为圆心,半径为1的圆的内接正方形,将一颗豆子随机
为圆心,半径为1的圆的内接正方形,将一颗豆子随机 (阴影部分)内”,则(1)
(阴影部分)内”,则(1) ;(2)
;(2)
 表示的区
表示的区 域为
域为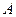 ,
,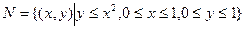 表示的区域为
表示的区域为 ,
, .
.