题目内容
3.已知抛物线E:x2=4y,m、n是过点A(a,-1)且倾斜角互补的两条直线,其中m与E有唯一公共点B,n与E相交于不同的两点C,D.(Ⅰ)求m的斜率k的取值范围;
(Ⅱ)是否存在常数λ,使得|AC|•|AD|=λ|AB|2?若存在,求λ的值;若不存在,说明理由.
分析 (Ⅰ)设直线m:y+1=k(x-a),n:y+1=-k(x-a),代入抛物线方程,运用判别式等于0和大于0,解不等式即可得到k的范围;
(Ⅱ)假设存在常数λ,使得|AC|•|AD|=λ|AB|2,设B(x0,y0),C(x1,y1),D(x2,y2),代入直线方程,由条件结合二次方程的韦达定理,再由判别式为0,即可判断.
解答 解:(Ⅰ)设直线m:y+1=k(x-a),n:y+1=-k(x-a),
分别代入x2=4y,得
x2-4kx+4ka+4=0(1),x2+4kx-4ka+4=0(2),
由△1=0得k2-ka-1=0,
由△2>0得k2+ka-1>0,
故有2k2-2>0,得k2>1,即k<-1,或k>1.
(Ⅱ)假设存在常数λ,使得|AC|•|AD|=λ|AB|2,
设B(x0,y0),C(x1,y1),D(x2,y2),
则(y1+1)(y2+1)=λ(y0+1)2.
将y1+1=-k(x1-a),y2+1=-k(x2-a),y0+1=k(x0-a)代入上式,得
(x1-a)(x2-a)=λ(x0-a)2,
即x1x2-a(x1+x2)+a2=λ(x0-a)2.
由(2)得x1+x2=-4k,x1x2=-4ka+4,
由(1)得x0=2k,代入上式,得
4+a2=λ(4k2-4ka+a2).
又△1=0得k2-ka-1=0,即4k2-4ka=4,
因此4+a2=λ(4+a2),λ=1.
故存在常数λ=1,使得|AC|•|AD|=λ|AB|2.
点评 本题考查抛物线的方程和性质,主要考查直线和抛物线方程联立,运用判别式和韦达定理,考查运算化简的能力,属于中档题.

练习册系列答案
相关题目
18.一种团体竞技比赛的积分规则是:每队胜、平、负分别得2分、1分、0分,已知甲球队已赛4场,积4分,在这4场比赛中,甲球队胜、平、负(包括顺序)的情况共有( )
| A. | 7种 | B. | 13种 | C. | 18种 | D. | 19种 |
15.已知z是复数,i是虚数单位,若zi=1+i,则z=( )
| A. | 1+i | B. | 1-i | C. | -1+i | D. | -1-i |
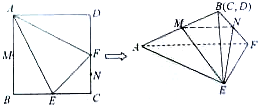 在边长为4的正方形ABCD中,E、F分别是BC、CD的中点,M、N分别是AB、CF的中点,将该正方形沿AE、AF、EF折叠,使B、C、D三点重合,构成一个三棱锥,如图所示.
在边长为4的正方形ABCD中,E、F分别是BC、CD的中点,M、N分别是AB、CF的中点,将该正方形沿AE、AF、EF折叠,使B、C、D三点重合,构成一个三棱锥,如图所示.