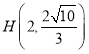题目内容
【题目】销售甲、乙两种商品所得利润分别是![]() 万元,它们与投入资金
万元,它们与投入资金![]() 万元的关系分别为
万元的关系分别为![]() (其中m,a,b都为常数),函数
(其中m,a,b都为常数),函数![]() 对应的曲线
对应的曲线![]() 如图所示.
如图所示.

(1)求函数![]() 与
与![]() 的解析式;
的解析式;
(2)若该商场一共投资10万元经销甲、乙两种商品,求该商场所获利润的最大值.
【答案】(1) ![]() ,
,![]() ,
, ![]() (2)
(2) ![]()
【解析】
试题分析:(1)根据所给的图象知,列出关于m,a的方程组![]() ,解出m,a的值,即可得到函数
,解出m,a的值,即可得到函数![]() 的解析式;(2)对甲种商品投资x(万元),对乙种商品投资(10-x)(万元),根据公式可得甲、乙两种商品的总利润y(万元)关于x的函数表达式;再利用配方法确定函数的对称轴,结合函数的定义域,即可求得总利润y的最大值
的解析式;(2)对甲种商品投资x(万元),对乙种商品投资(10-x)(万元),根据公式可得甲、乙两种商品的总利润y(万元)关于x的函数表达式;再利用配方法确定函数的对称轴,结合函数的定义域,即可求得总利润y的最大值
试题解析:(1)由题意![]() ,解得
,解得![]() , …………….2分
, …………….2分
![]() ……… ………………………3分
……… ………………………3分
又由题意![]() 得
得![]() ,
,![]() ,
, ![]() ………………………………………5分
………………………………………5分
(不写定义域或只写一个扣一分)
(2)设销售甲商品投入资金![]() 万元,则乙投入(
万元,则乙投入(![]() )万元
)万元
由(1)得![]() ………………7分
………………7分
令![]() 则有
则有![]()
![]() ,
,![]() …………9分
…………9分
当![]() 即
即![]() 时,
时,![]() 取最大值
取最大值![]() …………………11分
…………………11分
答:该商场所获利润的最大值为![]() 万元.(不答扣一分)……………………12分
万元.(不答扣一分)……………………12分

练习册系列答案
相关题目
【题目】某车间将10名技工平均分为甲,乙两组加工某种零件,在单位时间内每个技工加工零件若干,其中合格零件的个数如下表:
1号 | 2号 | 3号 | 4号 | 5号 | |
甲组 | 4 | 5 | 7 | 9 | 10 |
乙组 | 5 | 6 | 7 | 8 | 9 |
(1)分别求出甲,乙两组技工在单位时间内完成合格零件的平均数及方差,并由此判断哪组工人的技术水平更好;
(2)质监部门从该车间甲,乙两组中各随机抽取1名技工,对其加工的零件进行检测,若两人完成合格零件个数之和超过12件,则称该车间“质量合格”,否则“不合格”.求该车间“质量不合格”的概率.