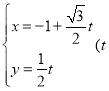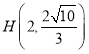题目内容
【题目】如图,已知椭圆![]() 的离心率
的离心率![]() ,长轴长为4.
,长轴长为4.

(1)求椭圆![]() 的方程;
的方程;
(2)设动直线![]() 与椭圆
与椭圆![]() 有且只有一个公共点
有且只有一个公共点![]() ,过右焦点
,过右焦点![]() 作直线
作直线![]() 与直线
与直线![]() 交与点
交与点![]() ,且
,且![]() .求证:点
.求证:点![]() 在定直线上,并求出定直线方程.
在定直线上,并求出定直线方程.
【答案】(1)![]() ;(2)证明见解析,
;(2)证明见解析,![]() .
.
【解析】
试题分析:(1)根据条件直接求出![]() 的值即可;(2)联立直线方程和椭圆方程,消去
的值即可;(2)联立直线方程和椭圆方程,消去![]() 得到
得到![]() ,由判别式等于
,由判别式等于![]() 整理得到
整理得到![]() ,代入
,代入![]() 求得
求得![]() 的坐标,然后写出直线
的坐标,然后写出直线![]() 方程为
方程为![]() ,联立方程组
,联立方程组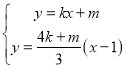 ,求得
,求得![]() ,即说明点
,即说明点![]() 在定直线
在定直线![]() 上.
上.
试题解析:(1)由椭圆的离心率![]() ,长轴长为4可知
,长轴长为4可知![]() ,
,
所以![]() ,∴椭圆
,∴椭圆![]() 的方程为
的方程为![]() ..............5分
..............5分
(2)由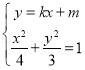 ,得方程
,得方程![]() (*).................6分
(*).................6分
由直线与椭圆相切,得![]() ,且
,且![]() 整理得;
整理得;
![]() ,将
,将![]() 代入(*)式,得
代入(*)式,得![]() ,
,
即![]() ,解得
,解得![]() ,∴
,∴![]() ,.............8分
,.............8分
又![]() ,①当
,①当![]() 即
即![]() ,∴
,∴![]() ②,
②,
②当![]() 时,∴
时,∴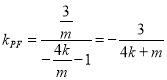 ,则
,则![]() ,...........9分
,...........9分
∴直线![]() 方程为
方程为![]() ,
,
联立方程组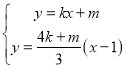 ,得
,得![]() ,
,
∴点![]() 在定直线
在定直线![]() 上...............................12分
上...............................12分

练习册系列答案
相关题目
【题目】某车间将10名技工平均分为甲,乙两组加工某种零件,在单位时间内每个技工加工零件若干,其中合格零件的个数如下表:
1号 | 2号 | 3号 | 4号 | 5号 | |
甲组 | 4 | 5 | 7 | 9 | 10 |
乙组 | 5 | 6 | 7 | 8 | 9 |
(1)分别求出甲,乙两组技工在单位时间内完成合格零件的平均数及方差,并由此判断哪组工人的技术水平更好;
(2)质监部门从该车间甲,乙两组中各随机抽取1名技工,对其加工的零件进行检测,若两人完成合格零件个数之和超过12件,则称该车间“质量合格”,否则“不合格”.求该车间“质量不合格”的概率.