题目内容
【题目】设双曲线 
（a＞0，b＞0）的左焦点为F1 ， 左顶点为A，过F1作x轴的垂线交双曲线于P、Q两点，过P作PM垂直QA于M，过Q作QN垂直PA于N，设PM与QN的交点为B，若B到直线PQ的距离大于a+ 
，则该双曲线的离心率取值范围是（ ）
A.（1﹣ 
）
B.（ ，+∞）
C.（1，2 ）
D.（2 ，+∞）
【答案】B
【解析】解：由题意可知：A（﹣a，0），P（﹣c， 
），Q（﹣c，﹣ ）， 由双曲线的对称性可知B在x轴上，设B（x，0），
则BP⊥AQ，
则kBPkAQ=﹣1，
∴ 
=﹣1，
则c+x=﹣ 
，
由B到直线PQ的距离d=x+c，
∴丨﹣ 丨＞a+ 
，则 
＞c2﹣a2=b2 ，
∴ 
＞1，
由椭圆的离心率e= 
= 
＞ 
，
双曲线的离心率取值范围（ ，+∞），
故选B．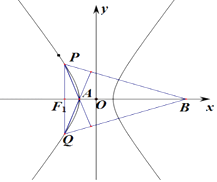
练习册系列答案
培优好卷单元加期末卷系列答案
一线名师权威作业本系列答案
相关题目
【题目】某学校高三年级有学生1 000名，经调查，其中750名同学经常参加体育锻炼(称为A类同学)，另外250名同学不经常参加体育锻炼(称为B类同学)，现用分层抽样方法(按A类、B类分两层)从该年级的学生中共抽查100名同学，如果以身高达165 cm作为达标的标准，对抽取的100名学生，得到以下列联表：
身高达标 | 身高不达标 | 总计 | |
经常参加体育锻炼 | 40 | ||
不经常参加体育锻炼 | 15 | ||
总计 | 100 |
（1）完成上表；
（2）能否在犯错误的概率不超过0.05的前提下认为经常参加体育锻炼与身高达标有关系(K2的观测值精确到0.001)?
