题目内容
【题目】四棱锥P﹣ABCD的三视图如图所示，其五个顶点都在同一球面上，若四棱锥P﹣ABCD的侧面积等于4（1+ 
），则该外接球的表面积是（ ） 
A.4π
B.12π
C.24π
D.36π
【答案】B
【解析】解：设正方体棱长为a，则由四棱锥P﹣ABCD的侧面积等于4（1+ 
），可得，a=2，设O是PC中点，则OA=OB=OC=OP= 
， 所以，四棱锥P﹣ABCD外接球球心与正方体外接球球心重合．
所以S= 
=12π，
故选B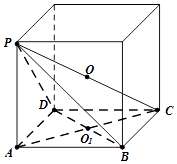
将三视图还原为直观图，得四棱锥P﹣ABCD的五个顶点位于同一个正方体的顶点处，且与该正方体内接于同一个球．由此结合题意，可得正方体的棱长为2，算出外接球半径R，再结合球的表面积公式，即可得到该球表面积．
练习册系列答案
相关题目
