已知正方形ABCD的边长为1.设$\overrightarrow{AB}=\vec a.\overrightarrow{BC}=\overrightarrow b.\overrightarrow{AC}=\vec c$.则$\vec a-\vec b+\vec c$的模为2．题目和参考答案——青夏教育精英家教网——

题目内容

5．已知正方形ABCD的边长为1，设$\overrightarrow{AB}=\vec a，\overrightarrow{BC}=\overrightarrow b，\overrightarrow{AC}=\vec c$，则$\vec a-\vec b+\vec c$的模为2．

分析利用向量的三角形法则将所求变形，利用正方形的边对应的向量表示，即可求模．

解答解：正方形如图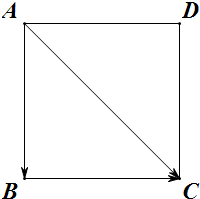，$\vec a-\vec b+\vec c$=$\overrightarrow{a}-\overrightarrow{b}+\overrightarrow{a}+\overrightarrow{b}$=2$\overrightarrow{a}$，
所以$\vec a-\vec b+\vec c$的模为2；
故答案为：2．

点评本题考查了平面向量的三角形法则；解得本题的关键是将所求利用正方形的两边对应的向量表示．

练习册系列答案

小学生每日10分钟系列答案

天利38套高中名校期中期末联考测试卷系列答案

口算题应用题天天练神机妙算系列答案

应用题点拨系列答案

培优新方法系列答案

状元及第系列答案

名师教你学数学系列答案

同步奥数系列答案

高中阶段三测卷系列答案

豫人教育单元检测系列答案

相关题目

15．由9个互不相等的正数组成的矩阵$（{\begin{array}{l}{{a_{11}}}&{{a_{12}}}&{{a_{13}}}\\{{a_{21}}}&{{a_{22}}}&{{a_{23}}}\\{{a_{31}}}&{{a_{32}}}&{{a_{33}}}\end{array}}）$中，每行中的三个数成等差数列，且a₁₁+a₁₂+a₁₃，a₂₁+a₂₂+a₂₃，a₃₁+a₃₂+a₃₃成等比数列，下列四个判断正确的个数为4个．
①第2列a₁₂，a₂₂，a₃₂必成等比数列
②第1列a₁₁，a₂₁，a₃₁不一定成等比数列
③a₁₂+a₃₂＞a₂₁+a₂₃
④若9个数之和等于9，则a₂₂＜1．

16．已知M是△ABC内的一点，且|AB||AC|=4，∠BAC=30°，若△MBC，△MCA，△MAB的面积分别为$\frac{1}{2}$、x、y，则$\frac{1}{x}$+$\frac{4}{y}$的最小值为（　　）

13．设数列{a_n}的前n项和为S_n，若S_n=2ⁿ-3，则数列{a_n}的通项公式为${a}_{n}=\left\{\begin{array}{l}{-1，n=1}\\{{2}^{n-1}，n≥2}\end{array}\right.$．

20．已知α为第二象限角，$sinα+cosα=\frac{1}{5}$，则cos2α=（　　）

$-\frac{12}{25}$

$-\frac{7}{25}$

10．命题p：?x∈R，使得3^x＞x；命题q：若函数y=f（x-1）为偶函数，则函数y=f（x）关于直线x=1对称，则（　　）

17．化简（x-4）⁴+4（x-4）³+6（x-4）²+4（x-4）+1得（　　）

x⁴

x⁵

14．复数z=$\frac{（1+i）^{2}}{1-i}$的共轭复数所对应的点位于复平面的（　　）

16．已知向量$\overrightarrow{a}$=（1，2）与$\overrightarrow{b}$=（λ，1）垂直，则λ=-2．