Question

四棱锥S-ABCD的底面ABCD是正方形，侧棱SC的中点E在底面内的射影恰好是正方形ABCD的中心O，顶点A在截面SBD内的射影恰好是△SBD的重心G．
（1）求直线SO与底面ABCD所成角的正切值；
（2）设AB=a，求此四棱锥过点C，D，G的截面面积．

Answer 1

（1）∵O、E分别是AC、SC的中点
∴SA∥EO则SA⊥面ABCD
∴∠SOA是SO与面ABCD所成角
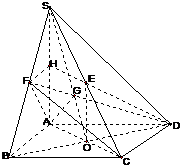∴SA，AB，AD两两相互垂直，连接DG并延长交SB于F．
∵SO是△SBD的中线，∴G点在SO上
∵AD⊥面SAB，AG⊥面SDB
∴AD⊥SB，AG⊥SB
则SB⊥面FAD即DF⊥SB
同理可得SO⊥BD，BG⊥SD
∴G是△SBD的垂心∴△SBD是等边三角形
∴SA=AB=AD∴tan∠SOA=

2

（2）G 是△SBD的重心，F是SB的中点
∵CD∥AB∴CD∥面SAB而过CDG的平面交面SAB与FH
∴CD⊥面SAD则四边形CDHF是直角梯形
梯形的高DH=

a2+ 1 4 a2

=

5

2

a
∴S_梯形CDHF=

3 5

8

a2