题目内容
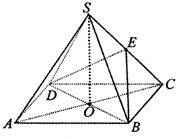
如图,四棱锥S-ABCD中,底面ABCD是边长为4的正方形,O是AC与BD的交点,SO⊥平面ABCD,E是侧棱SC的中点,异面直线SA和BC所成角的大小是60°.
(Ⅰ)求证:直线SA∥平面BDE;
(Ⅱ)求直线BD与平面SBC所成角的正弦值.
(Ⅰ)求证:直线SA∥平面BDE;
(Ⅱ)求直线BD与平面SBC所成角的正弦值.

(I)如图,连接EO,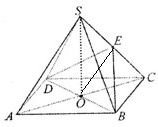
∵四棱锥S-ABCD中,底面ABCD是边长为4的正方形,O是AC与BD的交点,
∴O是AC的中点,
∵E是侧棱SC的中点,
∴EO是△ASC的中位线,
∴EO∥SA,
∵SA?面ASC,EO不包含于面ASC,
∴直线SA∥平面BDE.
(II)过点O作CB的平行线作x轴,过O作AB的平行线作y轴,以OS为z轴,建立如图所示的空间直角坐标系,
∵四棱锥S-ABCD中,底面ABCD是边长为4的正方形,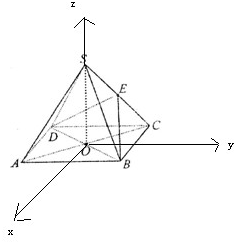
O是AC与BD的交点,SO⊥平面ABCD,E是侧棱SC的中点,
异面直线SA和BC所成角的大小是60°,
∴SA=4,SO=2
,
∴B(2,2,0),C(-2,2,0),S(0,0,2
),D(-2,-2,0),
∴
=(2,2,-2
),
=(-2,2,-2
),
=(-4,-4,0),
设面SBC的法向量为
=(x,y,z),
则
•
=0,
•
=0,
∴
,
∴
=(0,
,1),
设直线BD与平面SBC所成角为θ,
则sinθ=|cos<
,
>|=|
|=
.

∵四棱锥S-ABCD中,底面ABCD是边长为4的正方形,O是AC与BD的交点,
∴O是AC的中点,
∵E是侧棱SC的中点,
∴EO是△ASC的中位线,
∴EO∥SA,
∵SA?面ASC,EO不包含于面ASC,
∴直线SA∥平面BDE.
(II)过点O作CB的平行线作x轴,过O作AB的平行线作y轴,以OS为z轴,建立如图所示的空间直角坐标系,
∵四棱锥S-ABCD中,底面ABCD是边长为4的正方形,

O是AC与BD的交点,SO⊥平面ABCD,E是侧棱SC的中点,
异面直线SA和BC所成角的大小是60°,
∴SA=4,SO=2
| 2 |
∴B(2,2,0),C(-2,2,0),S(0,0,2
| 2 |
∴
| SB |
| 2 |
| SC |
| 2 |
| BD |
设面SBC的法向量为
| n |
则
| SB |
| n |
| SC |
| n |
∴
|
∴
| n |
| 2 |
设直线BD与平面SBC所成角为θ,
则sinθ=|cos<
| BD |
| n |
-4
| ||||
4
|
| ||
| 3 |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目