题目内容
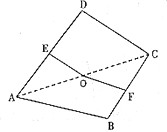
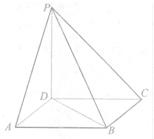
如图,四边形ABCD为正方形,PD⊥平面ABCD,PD=AD=2.
(1)求PC与平面PBD所成的角;
(2)在线段PB上是否存在一点E,使得PC⊥平面ADE?并说明理由.
(1)求PC与平面PBD所成的角;
(2)在线段PB上是否存在一点E,使得PC⊥平面ADE?并说明理由.

连接AC,设AC∩BD=O,连接PO
∵PD⊥平面ABCD,CO?平面ABCD∴PD⊥CO
由ABCD为正方形,知CO⊥BD
∵PD∩BD=D∴CO⊥平面PBD
∴∠CPO是直线PC与平面PBD所成的角
在Rt△POC中,sin∠CPO=
=
=
∴∠CPO=
∴直线PC与平面PBD所成的角为
(2)建立如图所示的空间直角坐标系D_xyz,设线段PB上存在一点E,使得PC⊥平面ADE
则存在实数λ,使得
=λ
(0≤λ≤1)
∵P(0,0,2),B(2,2,0)∴
=(2,2,-2)
∴
=
+
=
+λ
=(0,0,2)+(2λ,2λ,-2λ)=(2λ,2λ,2-2λ)
由题意显然有AD⊥平面PCD∴PC⊥AD 要使PC⊥平面ADE,只需
⊥
即
•
=0∴0×2λ+2×2λ-2(2-2λ)=0
∴λ=
∈[0,1]
故在线段上存在一点E(E为线段的中点)使得PC⊥平面ADE

∵PD⊥平面ABCD,CO?平面ABCD∴PD⊥CO
由ABCD为正方形,知CO⊥BD
∵PD∩BD=D∴CO⊥平面PBD
∴∠CPO是直线PC与平面PBD所成的角
在Rt△POC中,sin∠CPO=
| CO |
| CP |
| ||
2
|
| 1 |
| 2 |
∴∠CPO=
| π |
| 6 |
∴直线PC与平面PBD所成的角为
| π |
| 6 |
(2)建立如图所示的空间直角坐标系D_xyz,设线段PB上存在一点E,使得PC⊥平面ADE
则存在实数λ,使得
| PE |
| PB |
∵P(0,0,2),B(2,2,0)∴
| PB |
∴
| DE |
| DP |
| PE |
| DP |
| PB |
由题意显然有AD⊥平面PCD∴PC⊥AD 要使PC⊥平面ADE,只需
| PC |
| DE |
即
| PC |
| DE |
∴λ=
| 1 |
| 2 |
故在线段上存在一点E(E为线段的中点)使得PC⊥平面ADE


练习册系列答案
相关题目