题目内容
1.已知0<α<$\frac{π}{2}$,$\frac{π}{3}$<β<π,那么α+β的取值范围为$(\frac{π}{3},\frac{3π}{2})$.分析 直接利用不等式的基本性质求解即可.
解答 解:0<α<$\frac{π}{2}$,$\frac{π}{3}$<β<π,那么α+β∈$(\frac{π}{3},\frac{3π}{2})$.
故答案为:$(\frac{π}{3},\frac{3π}{2})$.
点评 本题考查不等式的基本性质的应用,考查计算能力.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案
相关题目
9.已知实数x,y满足方程x2+y2-4x+1=0,求:
(1)$\frac{y}{x}$的最大值和最小值;
(2)y-x的最小值;
(3)x2+y2的最大值和最小值;
(4)2x2+y2-4x-6的最大值.
(1)$\frac{y}{x}$的最大值和最小值;
(2)y-x的最小值;
(3)x2+y2的最大值和最小值;
(4)2x2+y2-4x-6的最大值.
10.下列说法错误的是 ( )
| A. | 平面直角坐标系内,每一条直线都有一个确定的倾斜角 | |
| B. | 每一条直线的斜率都是一个确定的值 | |
| C. | 没有斜率的直线是存在的 | |
| D. | 同一直线的斜率与倾斜角不是一一对应的 |
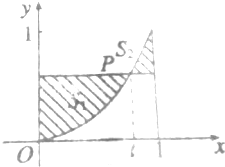 如图,在曲线C:y=x2,x∈[0,1]上取点P(t,t2),过点P作x轴的平行线l,曲线C于直线x=0,x=1及直线l围成的图形面积分别记为S1、S2.
如图,在曲线C:y=x2,x∈[0,1]上取点P(t,t2),过点P作x轴的平行线l,曲线C于直线x=0,x=1及直线l围成的图形面积分别记为S1、S2.