题目内容
【题目】已知函数f（x）=2x+m21﹣x ．
（1）若函数f（x）为奇函数，求实数m的值；
（2）若函数f（x）在区间（1，+∞）上是单调递增函数，求实数m的取值范围；
（3）是否存在实数a，使得函数f（x）的图象关于点A（a，0）对称，若存在，求实数a的值，若不存在，请说明理由．
注：点M（x1 ， y1），N（x2 ， y2）的中点坐标为（ 
， ）．
【答案】
（1）解：函数的定义域为实数集R
因为函数为奇函数
故f（﹣x）=﹣f（x），
所以f（0）=1+2m=0，即m=﹣ 
，
此时f（x）=2x﹣2﹣x．
函数为奇函数满足题意
故m=﹣
（2）解：解法一：
任取设1＜x1＜x2，
则f（x1）﹣f（x2）=（ 
）﹣（ 
）
=（ 
）（ 
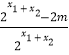）＜0对任意满足1＜x1＜x2恒成立
因为 ＜0，且 
，
故2m≤4，即m≤2；
解法二：若函数f（x）在区间（1，+∞）上是单调递增函数，
则f′（x）=ln22x﹣ln2m21﹣x≥0在区间（1，+∞）上恒成立，
即m≤22x﹣1在区间（1，+∞）上恒成立，
令y=22x﹣1，则在区间（1，+∞）上y＞22﹣1=2恒成立，
故m≤2
（3）解：假设存在满足条件的实数a
在函数f（x）图象上任取一点M（x1，y1），关于A（a，0）对称点为N（x2，y2）
则 
=a， 
=0，
即x2=2a﹣x1，y2=﹣y1，
即有f（x1）+f（2a﹣x1）=0恒成立
（注：没有推导过程的，只有结论的不给分）
即（ ）+ 
=0，
化简得：（22a+2m）（ 
+ 
）=0
∵ + ＞0恒成立，
故有：22a+2m=0，
当m≥0时，方程无解，故不存在
当m＜0时，a= 
，
综上所述：①当m≥0时，不存在实数a，使得函数f（x）图象关于点A（a，0）对称
②当m＜0时，存在实数a= ，使得得函数f（x）图象关于点A（a，0）对称
【解析】（1）由函数f（x）为奇函数，f（0）=0，解得实数m的值；（2）若函数f（x）在区间（1，+∞）上是单调递增函数，
解法一：f（x1）﹣f（x2）＜0对任意满足1＜x1＜x2恒成立，解得实数m的取值范围；
解法二：f′（x）≥0在区间（1，+∞）上恒成立，解得实数m的取值范围；（3）假设存在满足条件的实数a，则有有f（x1）+f（2a﹣x1）=0恒成立，则有：22a+2m=0，进而可得满足条件的答案．
【考点精析】通过灵活运用函数单调性的判断方法和函数的奇偶性，掌握单调性的判定法：①设x1,x2是所研究区间内任两个自变量，且x1＜x2；②判定f(x1)与f(x2)的大小；③作差比较或作商比较；偶函的图象关于y轴对称；奇函数的图象关于原点对称即可以解答此题．
