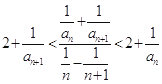Question

【题目】已知二次函数对都满足且，设函数（， ）．

（Ⅰ）求的表达式；

（Ⅱ）若，使成立，求实数m的取值范围；

（Ⅲ）设， ，求证：对于

恒有

Answer 1

【答案】（Ⅰ）（Ⅱ）（Ⅲ）见解析

【解析】试题分析：（Ⅰ）设，根据=直接可得答案．（Ⅱ）表示出函数f（x）的解析式，对m进行大于0、小于、和等于0进行分析可得答案．（Ⅲ）先根据H（x）的导数小于等于0判断出H（x）单调递减的，只要证明|H（m）-H（1）|<1即可．

试题解析：

（Ⅰ）设，于是

所以 又，则．所以．

（Ⅱ）

当m>0时，由对数函数性质，f（x）的值域为R；

当m=0时， 对， 恒成立；

当m<0时，由，列表：

x
	－	0	＋
	减	极小	增

由题意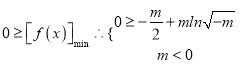

故使成立，实数m的取值范围）．

（Ⅲ）因为对， 所以在内单调递减．

于是

.

记，则

所以函数在是单调增函数，

所以，故命题成立．