题目内容
【题目】为庆祝党的98岁生日,某高校组织了“歌颂祖国,紧跟党走”为主题的党史知识竞赛。从参加竞赛的学生中,随机抽取40名学生,将其成绩分为六段![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,到如图所示的频率分布直方图.
,到如图所示的频率分布直方图.

(1)求图中![]() 的值及样本的中位数与众数;
的值及样本的中位数与众数;
(2)若从竞赛成绩在![]() 与
与![]() 两个分数段的学生中随机选取两名学生,设这两名学生的竞赛成绩之差的绝对值不大于
两个分数段的学生中随机选取两名学生,设这两名学生的竞赛成绩之差的绝对值不大于![]() 分为事件
分为事件![]() ,求事件
,求事件![]() 发生的概率.
发生的概率.
(3)为了激励同学们的学习热情,现评出一二三等奖,得分在![]() 内的为一等奖,得分在
内的为一等奖,得分在![]() 内的为二等奖, 得分在
内的为二等奖, 得分在![]() 内的为三等奖.若将频率视为概率,现从考生中随机抽取三名,设
内的为三等奖.若将频率视为概率,现从考生中随机抽取三名,设![]() 为获得三等奖的人数,求
为获得三等奖的人数,求![]() 的分布列与数学期望.
的分布列与数学期望.
【答案】(1)0.06;87.5;87.5;(2)![]() ;(3)详见解析
;(3)详见解析
【解析】
(1)根据小矩形的面积之和等于1,列出方程,求得![]() 的值,根据中位数定义估计中位数的范围,在列出方程求解中位数,再根据众数的定义,即可求解.
的值,根据中位数定义估计中位数的范围,在列出方程求解中位数,再根据众数的定义,即可求解.
(2)计算两组的人数,再计算抽取的两人在同一组的概率,即可求解;
(3)根据题意,得到随机变量服从二项分布,再利用二项分布的期望公式,即可求解.
(1)由频率分布直方图可知![]() ,解得
,解得![]() ,
,
可知样本的中位数在第4组中,不妨设为![]() ,
,
则![]() ,解得
,解得![]() ,
,
即样本的中位数为![]() ,
,
由频率分布直方图可知,样本的众数为![]() .
.
(2)由频率分布直方图可知,在![]() 与
与![]() 两个分数段的学生人数分别为
两个分数段的学生人数分别为![]() 和
和![]() ,设中两名学生的竞赛成绩之差的绝对值不大于5分为事件M,
,设中两名学生的竞赛成绩之差的绝对值不大于5分为事件M,
则事件M发生的概率为![]() ,即事件M发生的概率为
,即事件M发生的概率为![]() .
.
(3)从考生中随机抽取三名,则随机变量![]() 为获得三等奖的人数,则
为获得三等奖的人数,则![]() ,
,
由频率分布直方图知,从考升中任抽取1人,此生获得三等奖的概率为![]() ,
,
所以随机变量服从二项分布![]() ,
,
则![]() ,
,
![]() ,
,
所以随机变量的分布列为
| 0 | 1 | 2 | 3 |
| 0.343 | 0.441 | 0.189 | 0.027 |
所以![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】某连锁经营公司所属5个零售店某月的销售额和利润额资料如下表
商店名称 | A | B | C | D | E |
销售额x(千万元) | 3 | 5 | 6 | 7 | 9 |
利润额y(百万元) | 2 | 3 | 3 | 4 | 5 |
(1)画出散点图.观察散点图,说明两个变量有怎样的相关性.
(2)用最小二乘法计算利润额y对销售额x的回归直线方程.
(3)当销售额为4(千万元)时,估计利润额的大小.
其中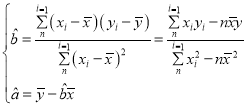
【题目】某同学用“五点法”画函数![]() 在某一个周期内的图象时,列表并填入了部分数据,如下表:
在某一个周期内的图象时,列表并填入了部分数据,如下表:
|
|
|
|
|
|
|
|
| |||
|
|
|
|
|
(1)请将上表数据补充完整;函数![]() 的解析式为
的解析式为![]() (直接写出结果即可);
(直接写出结果即可);
(2)根据表格中的数据作出![]() 一个周期的图象;
一个周期的图象;
(3)求函数![]() 在区间
在区间![]() 上的最大值和最小值.
上的最大值和最小值.