题目内容
设P1(x1,y1),P1(x2,y2),…,Pn(xn,yn)(n≥3,n∈N) 是二次曲线C上的点,且a1=|OP1|2,a2=|OP2|2,…,an=|OPn|2构成了一个公差为d(d≠0) 的等差数列,其中O是坐标原点.记Sn=a1+a2+…+an.
(1)若C的方程为 -y2=1,n=3.点P1(3,0) 及S3=162,求点P3的坐标;(只需写出一个)
-y2=1,n=3.点P1(3,0) 及S3=162,求点P3的坐标;(只需写出一个)
(2)若C的方程为y2=2px(p≠0).点P1(0,0),对于给定的自然数n,证明:(x1+p)2,(x2+p)2,…,(xn+p)2成等差数列;
(3)若C的方程为 (a>b>0).点P1(a,0),对于给定的自然数n,当公差d变化时,求Sn的最小值.
(a>b>0).点P1(a,0),对于给定的自然数n,当公差d变化时,求Sn的最小值.
| 符号意义 | 本试卷所用符号 | 等同于《实验教材》符号 |
| 向量坐标 |  ={x,y} ={x,y} |  =(x,y) =(x,y) |
| 正切 | tg | tan |
解:(1)a1=|OP1|2=9,由S3= (a1+a3)=162,得a3=|OP3|3=99.
(a1+a3)=162,得a3=|OP3|3=99.
由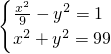 得
得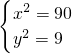
∴点P3的坐标可以为(3 ,3).
,3).
(2)对每个自然数k,1≤k≤n,由题意|OPk|2=(k-1)d,
及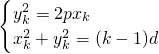
即(xk+p)2=p2+(k-1)d,
∴(x1+p)2,(x2+p)2,…(xn+p)2是首项为p2,公差为d的等差数列.
(3)原点O到二次曲线
C: (a>b>0)上各点的最小距离为b,最大距离为a.
(a>b>0)上各点的最小距离为b,最大距离为a.
∵a1=|OP1|2=a2,∴d<0,且an=|OPn|2=a2+(n-1)d≥b2,
∴ ≤d<0.∵n≥3,
≤d<0.∵n≥3, >0
>0
∴Sn=na2+ d在[
d在[ ,0)上递增,
,0)上递增,
故Sn的最小值为na2+ •
• =
= .
.
分析:(1)利用条件求出a3的值.再联立二次曲线求出点P3的坐标即可.
(2)先利用定义求出|OPk|2,再联立二次曲线求出(xk+p)2表达式,就可下结论.
(3)先求出原点O到二次曲线上各点的最小距离和最大距离;再利用定义求出an的通项以及Sn的表达式,利用公差d的范围,求出Sn的最小值即可.
点评:本题是对数列和函数以及二次曲线的综合考查.其中涉及到了等差数列的证明,数列的求和等知识点,是一道不太容易的题.
 (a1+a3)=162,得a3=|OP3|3=99.
(a1+a3)=162,得a3=|OP3|3=99.由
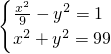 得
得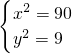
∴点P3的坐标可以为(3
 ,3).
,3).(2)对每个自然数k,1≤k≤n,由题意|OPk|2=(k-1)d,
及
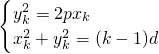
即(xk+p)2=p2+(k-1)d,
∴(x1+p)2,(x2+p)2,…(xn+p)2是首项为p2,公差为d的等差数列.
(3)原点O到二次曲线
C:
 (a>b>0)上各点的最小距离为b,最大距离为a.
(a>b>0)上各点的最小距离为b,最大距离为a.∵a1=|OP1|2=a2,∴d<0,且an=|OPn|2=a2+(n-1)d≥b2,
∴
 ≤d<0.∵n≥3,
≤d<0.∵n≥3, >0
>0∴Sn=na2+
 d在[
d在[ ,0)上递增,
,0)上递增,故Sn的最小值为na2+
 •
• =
= .
.分析:(1)利用条件求出a3的值.再联立二次曲线求出点P3的坐标即可.
(2)先利用定义求出|OPk|2,再联立二次曲线求出(xk+p)2表达式,就可下结论.
(3)先求出原点O到二次曲线上各点的最小距离和最大距离;再利用定义求出an的通项以及Sn的表达式,利用公差d的范围,求出Sn的最小值即可.
点评:本题是对数列和函数以及二次曲线的综合考查.其中涉及到了等差数列的证明,数列的求和等知识点,是一道不太容易的题.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
设P1(x1,y1),P1(x2,y2),…,Pn(xn,yn)(n≥3,n∈N) 是二次曲线C上的点,且a1=|OP1|2,a2=|OP2|2,…,an=|OPn|2构成了一个公差为d(d≠0) 的等差数列,其中O是坐标原点.记Sn=a1+a2+…+an.
(1)若C的方程为
-y2=1,n=3.点P1(3,0) 及S3=162,求点P3的坐标;(只需写出一个)
(2)若C的方程为y2=2px(p≠0).点P1(0,0),对于给定的自然数n,证明:(x1+p)2,(x2+p)2,…,(xn+p)2成等差数列;
(3)若C的方程为
+
=1(a>b>0).点P1(a,0),对于给定的自然数n,当公差d变化时,求Sn的最小值.
(1)若C的方程为
| x2 |
| 9 |
(2)若C的方程为y2=2px(p≠0).点P1(0,0),对于给定的自然数n,证明:(x1+p)2,(x2+p)2,…,(xn+p)2成等差数列;
(3)若C的方程为
| x2 |
| a2 |
| y2 |
| b2 |
| 符号意义 | 本试卷所用符号 | 等同于《实验教材》符号 | ||||
| 向量坐标 |
|
| ||||
| 正切 | tg | tan |
