题目内容
已知f是直角坐标平面xOy到自身的一个映射,点P在映射f下的象为点Q,记作Q=f(P).设P
1(x
1,y
1),P
2=f(P
1),P
3=f(P
2),…,P
n=f(P
n-1),….如果存在一个圆,使所有的点P
n(x
n,y
n)(n∈N
*)都在这个圆内或圆上,那么称这个圆为点P
n(x
n,y
n)的一个收敛圆.特别地,当P
1=f(P
1)时,则称点P
1为映射f下的不动点.若点P(x,y)在映射f下的象为点
Q(-x+1,y).
(Ⅰ)求映射f下不动点的坐标;
(Ⅱ)若P
1的坐标为(2,2),求证:点P
n(x
n,y
n)(n∈N
*)存在一个半径为2的收敛圆.
分析:(Ⅰ)设不动点的坐标为P
0(x
0,y
0),依据对应关系及不动点的定义,解方程组
,可得不动点的坐标.
(Ⅱ)由P
n+1=f(P
n),得
,构造两个等比数列
{xn-}(n∈N
*)和{y
n},
写出它们的通项公式,设
A(, 1),计算P
n到A的距离,可得此距离小于2,故所有的点P
n(n∈N
*)都在以
A(, 1)为圆心,2为半径的圆内.
解答:(Ⅰ)解:设不动点的坐标为P
0(x
0,y
0),
由题意,得
,解得
x0=, y0=0,
所以此映射f下不动点为
P0(, 0).
(Ⅱ)证明:由P
n+1=f(P
n),得
,
所以
xn+1-=-(xn-), yn+1=yn,
因为x
1=2,y
1=2,
所以
xn-≠0, yn≠0,
所以
=-1, =,
由等比数列定义,得数列
{xn-}(n∈N
*)是公比为-1,首项为
x1-=的等比数列,
所以
xn-=×(-1)n-1,则
xn=+(-1)n-1×.
同理
yn=2×()n-1.
所以
Pn(+(-1)n-1×, 2×()n-1).
设
A(, 1),则
|APn|=,
因为
0<2×()n-1≤2,
所以
-1≤1-2×()n-1<1,
所以
|APn|≤<2.
故所有的点P
n(n∈N
*)都在以
A(, 1)为圆心,2为半径的圆内,
即点P
n(x
n,y
n)存在一个半径为2的收敛圆.
点评:本题考查映射的定义,构造等比数列并求通项公式,两点间的距离公式的应用.
练习册系列答案
相关题目

 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案 ,P1(2,3),求证:点Pn(xn,yn)(n∈N*)存在一个半径为
,P1(2,3),求证:点Pn(xn,yn)(n∈N*)存在一个半径为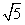 的收敛圆。
的收敛圆。