题目内容
16.已知圆C的圆心为坐标原点O,且与直线l1:x-y-2=0相切,(1)求圆C的方程;
(2)若与直线l1垂直的直线l2与圆交于不同的两点P、Q,且以PQ为直径的圆过原点,求直线l2的方程.
分析 (1)根据点到直线的距离确定圆的半径,则圆的方程可得.
(2)设出直线l2的方程,判断出△OPQ为等腰直角三角形,求得圆心到直线l2的距离进而利用点到直线的距离求得c.则直线方程可得.
解答 解:(1)由已知圆心到直线的距离为半径,求得半径r=$\frac{2}{\sqrt{1+1}}$=$\sqrt{2}$,
∴圆的方程为x2+y2=2.
(2)设直线l2的方程为x+y+c=0,
由已知△OPQ为等腰直角三角形,则圆心到直线l2的距离为1,利用点到直线的距离公式得$\frac{|c|}{\sqrt{2}}$=1,
求得c=±$\sqrt{2}$.
所以直线l2的方程为x+y+$\sqrt{2}$=0或x+y-$\sqrt{2}$=0.
点评 本题主要考查了直线与圆的方程的应用.注意数形结合思想的灵活运用.

练习册系列答案
相关题目
11.设椭圆的两个焦点分别为F1,F2,过F2作椭圆长轴的垂线与椭圆相交,其中的一个交点为P,若△F1PF2为等腰直角三角形,则椭圆的离心率是( )
| A. | $\sqrt{3}$-1 | B. | $\sqrt{2}$-1 | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{2}}{2}$ |
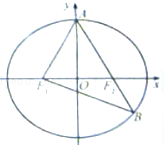 如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左右焦点分别为F1,F2,A是椭圆C的一
如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左右焦点分别为F1,F2,A是椭圆C的一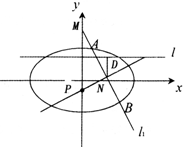 已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的长轴长是短轴长的$\sqrt{3}$倍,且经过点($\sqrt{3}$,1).
已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的长轴长是短轴长的$\sqrt{3}$倍,且经过点($\sqrt{3}$,1).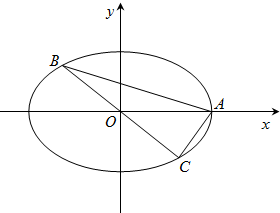 如图,A,B,C是椭圆M:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)上的三点,其中点A是椭圆的右顶点,BC过椭圆M的中心,且满足AC⊥BC,BC=2AC.
如图,A,B,C是椭圆M:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)上的三点,其中点A是椭圆的右顶点,BC过椭圆M的中心,且满足AC⊥BC,BC=2AC.