题目内容
在直角坐标平面中,△ABC的两个顶点为 A(0,-1),B(0, 1)平面内两点G、M同时满足①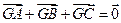 , ②
, ②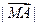 =
= 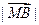 =
= 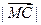 ③
③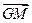 ∥
∥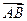
(1)求顶点C的轨迹E的方程
(2)设P、Q、R、N都在曲线E上 ,定点F的坐标为(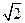 , 0) ,已知
, 0) ,已知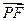 ∥
∥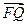 ,
,
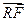 ∥
∥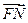 且
且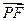 ·
·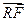 = 0.求四边形PRQN面积S的最大值和最小值.
= 0.求四边形PRQN面积S的最大值和最小值.
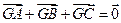 , ②
, ②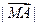 =
= 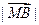 =
= 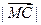 ③
③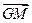 ∥
∥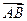
(1)求顶点C的轨迹E的方程
(2)设P、Q、R、N都在曲线E上 ,定点F的坐标为(
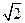 , 0) ,已知
, 0) ,已知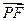 ∥
∥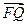 ,
, 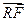 ∥
∥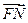 且
且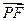 ·
·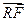 = 0.求四边形PRQN面积S的最大值和最小值.
= 0.求四边形PRQN面积S的最大值和最小值. (1) 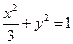 (x≠0)(2) Smax =" 2" , Smin =
(x≠0)(2) Smax =" 2" , Smin =  。
。
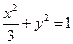 (x≠0)(2) Smax =" 2" , Smin =
(x≠0)(2) Smax =" 2" , Smin =  。
。(1)设C ( x , y ), 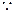
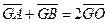 ,由①知
,由①知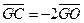 ,
,
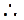 G为△ABC的重心 ,
G为△ABC的重心 ,  G(
G(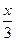 ,
,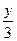 )
)
由②知M是△ABC的外心, M在x轴上
M在x轴上
由③知M(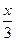 ,0),
,0),
由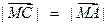 得
得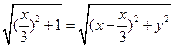
化简整理得: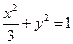 (x≠0 )
(x≠0 )
(2)F(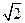 ,0 )恰为
,0 )恰为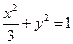 的右焦点
的右焦点
设PQ的斜率为k≠0且k≠±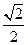 ,则直线PQ的方程为y =" k" ( x -
,则直线PQ的方程为y =" k" ( x -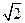 )
)
由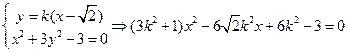
设P(x1 , y1) ,Q (x2 ,y2 ) 则x1 + x2 =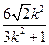 , x1·x2 =
, x1·x2 =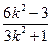
则| PQ | =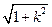 ·
· 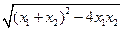 =
= 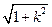 ·
·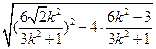
=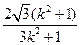
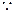 RN⊥PQ,把k换成
RN⊥PQ,把k换成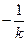 得 | RN
得 | RN
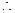 S =
S =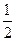 | PQ | · | RN |
| PQ | · | RN |
=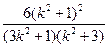
=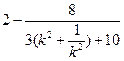 )
)
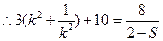
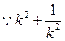 ≥2 ,
≥2 , 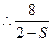 ≥16
≥16
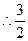 ≤ S < 2 , (当 k = ±1时取等号)
≤ S < 2 , (当 k = ±1时取等号)
又当k不存在或k = 0时S = 2
综上可得 ≤ S ≤ 2
≤ S ≤ 2
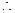 Smax =" 2" , Smin =
Smax =" 2" , Smin = 
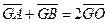 ,由①知
,由①知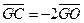 ,
,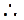 G为△ABC的重心 ,
G为△ABC的重心 , 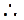 G(
G(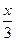 ,
,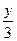 )
) 由②知M是△ABC的外心,
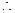 M在x轴上
M在x轴上由③知M(
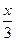 ,0),
,0),由
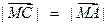 得
得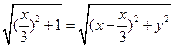
化简整理得:
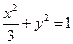 (x≠0 )
(x≠0 )(2)F(
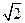 ,0 )恰为
,0 )恰为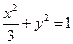 的右焦点
的右焦点设PQ的斜率为k≠0且k≠±
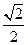 ,则直线PQ的方程为y =" k" ( x -
,则直线PQ的方程为y =" k" ( x -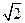 )
)由
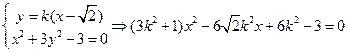
设P(x1 , y1) ,Q (x2 ,y2 ) 则x1 + x2 =
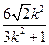 , x1·x2 =
, x1·x2 =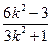
|
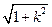 ·
· 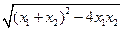 =
= 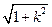 ·
·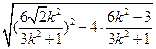
=
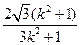
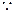 RN⊥PQ,把k换成
RN⊥PQ,把k换成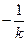 得 | RN
得 | RN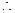 S =
S =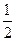 | PQ | · | RN |
| PQ | · | RN |=
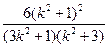
=
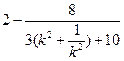 )
) 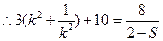
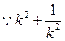 ≥2 ,
≥2 , 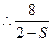 ≥16
≥16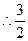 ≤ S < 2 , (当 k = ±1时取等号)
≤ S < 2 , (当 k = ±1时取等号) 又当k不存在或k = 0时S = 2
综上可得
 ≤ S ≤ 2
≤ S ≤ 2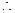 Smax =" 2" , Smin =
Smax =" 2" , Smin = 
|

练习册系列答案
相关题目
 ,
, .
. 来表示向量
来表示向量 ;
; ,
,
 )设
)设 ,当
,当 、
、 、
、 、
、 四点共圆时, 求
四点共圆时, 求 的值.
的值.
 共线的充分必要条件是存在实数
共线的充分必要条件是存在实数 使
使 成立。
成立。 车站,为适应客运需要准备新增
车站,为适应客运需要准备新增 个车站,则客运车票增加了
个车站,则客运车票增加了 种的必要条件是
种的必要条件是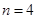 。
。 成立的充分必要条件是
成立的充分必要条件是 。
。 为全集,则
为全集,则 的充分条件是
的充分条件是 。
。 ②④
②④  ①②
①②  ①③
①③ 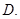 ③④
③④  ,
, 的值; (2)求
的值; (2)求 的夹角
的夹角 ; (3)求
; (3)求 .
.
 的取值范围;
的取值范围; ,
, ,求
,求 的值
的值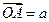 ,
, ,任意点
,任意点 关于点
关于点 的对称点为
的对称点为 ,点
,点 的对称点为
的对称点为 ,用
,用 、
、 表示向量
表示向量 .
.

 ,
, =
=