题目内容
已知椭圆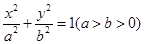 的左顶点为
的左顶点为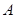 ,上顶点为
,上顶点为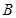 ,右焦点为
,右焦点为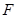 .设线段
.设线段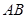 的中点为
的中点为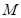 ,若
,若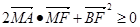 ,则该椭圆离心率的取值范围为 .
,则该椭圆离心率的取值范围为 .
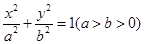 的左顶点为
的左顶点为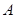 ,上顶点为
,上顶点为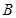 ,右焦点为
,右焦点为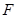 .设线段
.设线段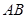 的中点为
的中点为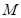 ,若
,若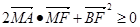 ,则该椭圆离心率的取值范围为 .
,则该椭圆离心率的取值范围为 .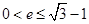
试题分析:因为
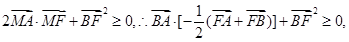
即
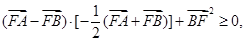
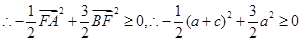 ,
,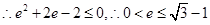 .
.点评:解本小题的关键是把题目的条件
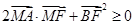 最终转化为
最终转化为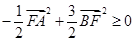 ,
,从而得到关于a,c的不等式,问题到此得解.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案
相关题目
题目内容
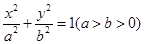 的左顶点为
的左顶点为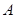 ,上顶点为
,上顶点为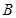 ,右焦点为
,右焦点为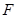 .设线段
.设线段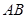 的中点为
的中点为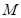 ,若
,若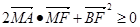 ,则该椭圆离心率的取值范围为 .
,则该椭圆离心率的取值范围为 .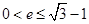
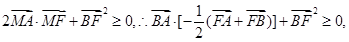
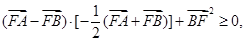
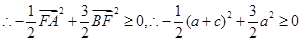 ,
,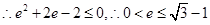 .
.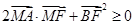 最终转化为
最终转化为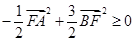 ,
,
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案