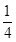题目内容
已知椭圆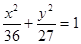 ,过右焦点F作不垂直于
,过右焦点F作不垂直于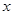 轴的弦交椭圆于A、B两点,AB的垂直平分线交
轴的弦交椭圆于A、B两点,AB的垂直平分线交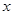 轴于N,则|NF|∶|AB|等于( )
轴于N,则|NF|∶|AB|等于( )
A.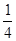 B.
B.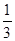 C.
C.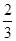 D.
D.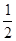
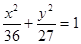 ,过右焦点F作不垂直于
,过右焦点F作不垂直于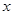 轴的弦交椭圆于A、B两点,AB的垂直平分线交
轴的弦交椭圆于A、B两点,AB的垂直平分线交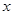 轴于N,则|NF|∶|AB|等于( )
轴于N,则|NF|∶|AB|等于( )A.
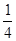 B.
B.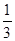 C.
C.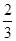 D.
D.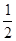
A
试题分析:根据已知条件,取直线的斜率为1.右焦点F(2,0).直线AB的方程为y=x-2.联立方程组
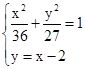 ,将y=x-2代入到椭圆中可知7x2-16x-92=0,设点设A(x1,y1),B(x2,y2),则x1+x2=
,将y=x-2代入到椭圆中可知7x2-16x-92=0,设点设A(x1,y1),B(x2,y2),则x1+x2=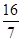 ,y1+y2=x1-2+x2-2=-
,y1+y2=x1-2+x2-2=-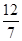 ,x1x2=-
,x1x2=-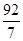 ,所以AB中点坐标为(
,所以AB中点坐标为(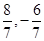 ),然后得到AB的垂直平分线方程,即为y+
),然后得到AB的垂直平分线方程,即为y+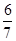 =-(x-
=-(x-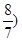 ,令y=0,得到x=
,令y=0,得到x=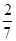 ,得到点N(
,得到点N(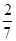 ,0),多以可知∴|NF|:|AB|=
,0),多以可知∴|NF|:|AB|=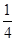 ,选A
,选A点评:特值法是求解选择题和填空题的有效方法.

练习册系列答案
相关题目
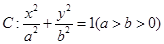 ,过焦点且垂直于长轴的弦长为1,且焦点与短轴两端点构成等边三角形.
,过焦点且垂直于长轴的弦长为1,且焦点与短轴两端点构成等边三角形.
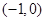 的直线
的直线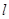 交椭圆于
交椭圆于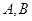 两点,交直线
两点,交直线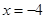 于点
于点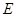 ,且
,且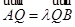 ,
,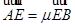 ,
,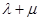 为定值,并计算出该定值.
为定值,并计算出该定值. 轴上的椭圆
轴上的椭圆 的离心率是
的离心率是 ,则
,则 的值为 ( )
的值为 ( )

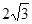

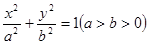 的顶点与焦点,若∠ ABC=90°,则该椭圆的离心率为 ( )
的顶点与焦点,若∠ ABC=90°,则该椭圆的离心率为 ( )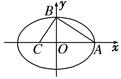


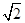 -1
-1  的两个焦点分别为
的两个焦点分别为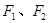 ,离心率为2.
,离心率为2.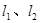 的方程;
的方程;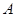 、
、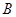 分别为
分别为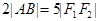 ,求线段
,求线段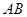 的中点
的中点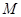 的轨迹方程,并说明轨迹是什么曲线;
的轨迹方程,并说明轨迹是什么曲线;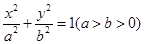 的左顶点为
的左顶点为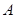 ,上顶点为
,上顶点为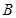 ,右焦点为
,右焦点为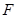 .设线段
.设线段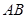 的中点为
的中点为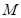 ,若
,若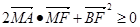 ,则该椭圆离心率的取值范围为 .
,则该椭圆离心率的取值范围为 .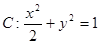 的两焦点为
的两焦点为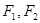 ,点
,点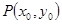 满足
满足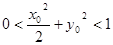 ,则
,则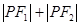 的取值范围为 ,直线
的取值范围为 ,直线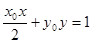 与椭圆
与椭圆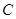 的公共点个数为 .
的公共点个数为 .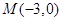 ,点
,点 ,动点
,动点 满足
满足 ,则点
,则点