题目内容
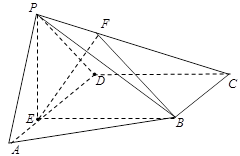
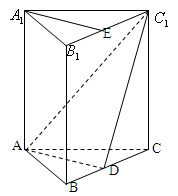
如图,在长方体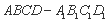 中,
中,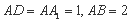 .
.
(1)若点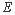 在对角线
在对角线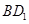 上移动,求证:
上移动,求证: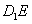 ⊥
⊥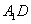 ;
;
(2)当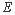 为棱
为棱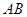 中点时,求点
中点时,求点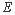 到平面
到平面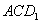 的距离。
的距离。
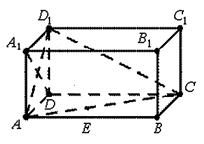
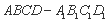 中,
中,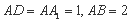 .
. (1)若点
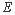 在对角线
在对角线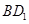 上移动,求证:
上移动,求证: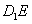 ⊥
⊥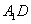 ;
;(2)当
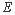 为棱
为棱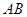 中点时,求点
中点时,求点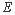 到平面
到平面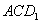 的距离。
的距离。 
(1)详见解析;(2) .
.
 .
.试题分析:(1)连结
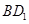 ,要证
,要证 ,只要证
,只要证 ,只要证
,只要证 平面
平面
事实上,在正方形
 中,
中, ,且有
,且有 ,从而有
,从而有 ,结论可证.
,结论可证.(2)连结
 ,因为
,因为 ,可利用等积法求点
,可利用等积法求点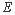 到平面
到平面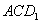 的距离.
的距离.证明:(1)由长方体
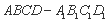 ,得:
,得: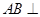 面
面
而

 面
面 ∴
∴ 即
即
又由正方形
 ,得:
,得: , 而
, 而
∴
 面
面 于是
于是
而
 即
即 6分
6分解:(2)
 过
过 作
作 垂直
垂直 于
于 ,则
,则
所以
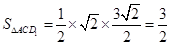 ,设点
,设点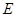 到平面
到平面 的距离为
的距离为
则由
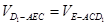 有
有 ,得
,得 12分
12分
练习册系列答案
相关题目
 中,
中, ⊥平面
⊥平面 ,
, ∥
∥ ,
, ,
, 分别为线段
分别为线段 的中点.
的中点.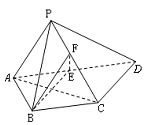
 ;
;  ⊥平面
⊥平面 .
.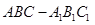 中,点
中,点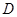 在边
在边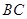 上,
上,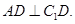
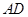
 平面
平面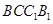 ;
; 是
是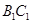 的中点,求证:
的中点,求证: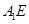 //平面
//平面 .
.
 底面是菱形,
底面是菱形, ,
, ,
, 分别是
分别是 的中点.
的中点.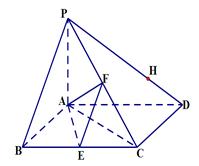
 ⊥平面
⊥平面 ;
;  是
是 上的动点,
上的动点, 与平面
与平面 ,求二面角
,求二面角 的正切值.
的正切值.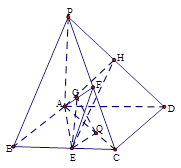
 ?
?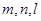 是直线,
是直线,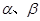 是平面,下列命题中,正确的命题是 .(填序号)
是平面,下列命题中,正确的命题是 .(填序号)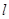 垂直于
垂直于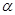 内两条直线,则
内两条直线,则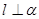 ;
; 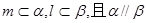 ,则
,则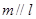 ;
; 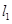 、
、 、
、 、
、 ,满足
,满足 ,
, ,
, ,则下列结论一定正确的是( )
,则下列结论一定正确的是( )

 、
、 是两个不同的平面.则下列命题中正确的是( )
是两个不同的平面.则下列命题中正确的是( )

 m⊥n
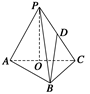
m⊥n 中,
中, 为
为 上一点,面
上一点,面 面
面 ,四边形
,四边形 为矩形
为矩形 ,
, ,
,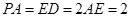 .
.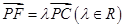 ,且
,且 ∥面
∥面 ,求
,求 的值;
的值; 面
面 ,并求点
,并求点 到面
到面 的距离.
的距离.