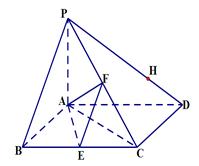
题目内容
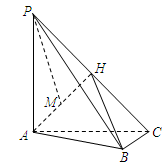
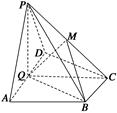
四棱锥 底面是菱形,
底面是菱形, ,
, ,
, 分别是
分别是 的中点.
的中点.
(1)求证:平面 ⊥平面
⊥平面 ;
;
(2) 是
是 上的动点,
上的动点, 与平面
与平面 所成的最大角为
所成的最大角为 ,求二面角
,求二面角 的正切值.
的正切值.
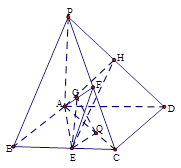
 底面是菱形,
底面是菱形, ,
, ,
, 分别是
分别是 的中点.
的中点.
(1)求证:平面
 ⊥平面
⊥平面 ;
; (2)
 是
是 上的动点,
上的动点,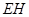 与平面
与平面 所成的最大角为
所成的最大角为 ,求二面角
,求二面角 的正切值.
的正切值.
(1)参考解析;(2)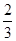
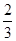
试题分析:(1)由已知可得直线AE垂直于BC,即可得到AE垂直于AD,又因为PA垂直于AE.所以可得AE垂直于平面PAD.即可得平面要证平面
 ⊥平面
⊥平面 .
.(2)通过点E作EG垂直于AF,EQ垂直于AC,连结QG即可证得
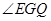 为所求的二面角的平面角.由
为所求的二面角的平面角.由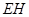 与平面
与平面 所成的最大角为
所成的最大角为 .可得AE=AH.即可得EQ,QG的大小.从求得
.可得AE=AH.即可得EQ,QG的大小.从求得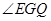 的正切值,即二面角
的正切值,即二面角  的正切值.
的正切值.(1)设菱形ABCD的边长为2a,则
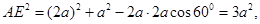 AE=
AE=
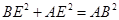 ,∴AE⊥BC,又AD||BC, ∴AE⊥AD.∵PA⊥面ABCD, ∴PA⊥AE,AE⊥面PAD, ∴面AEF⊥面PAD.
,∴AE⊥BC,又AD||BC, ∴AE⊥AD.∵PA⊥面ABCD, ∴PA⊥AE,AE⊥面PAD, ∴面AEF⊥面PAD.(2)过E作EQ⊥AC,垂足为Q,过作QG⊥AF,垂足为G,连GE,∵PA⊥面ABCD,∴PA⊥EQ,EQ⊥面PAC,则∠EGQ是二面角E-AF-C的平面角.
过点A作AH⊥PD,连接EH,∵ AE⊥面PAD,∴∠AHE是EH与面PAD所成的最大角.
∵∠AHE=
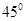 ,∴AH=AE=
,∴AH=AE= ,AH﹒PD=PA﹒AD,2a﹒PA=
,AH﹒PD=PA﹒AD,2a﹒PA= ﹒
﹒ ,PA=2
,PA=2 ,PC=4a,EQ=
,PC=4a,EQ=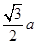 ,CQ=
,CQ=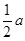 ,GQ=
,GQ=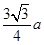 ,tan∠EGQ=
,tan∠EGQ=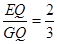 .
.
练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
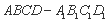 中,
中,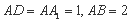 .
. 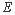 在对角线
在对角线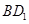 上移动,求证:
上移动,求证: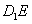 ⊥
⊥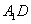 ;
;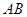 中点时,求点
中点时,求点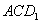 的距离。
的距离。 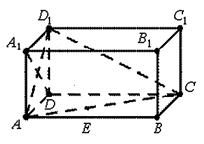
 中,
中, 底面
底面 ,
,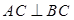 ,
, 为
为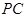 的中点,
的中点, 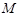 为
为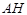 的中点,
的中点,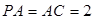 ,
,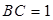 .
.
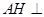 平面
平面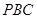 ;
;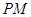 与平面
与平面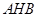 成角的正弦值;
成角的正弦值;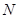 在线段
在线段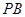 上,且
上,且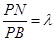 ,
,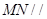 平面
平面 ,求实数
,求实数 的值.
的值. AD=1,CD=
AD=1,CD= .
.
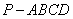 ,底面
,底面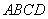 为菱形,
为菱形,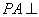 平面
平面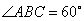 ,
, 分别是
分别是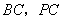 的中点.
的中点.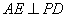 ;
; 为
为 上的动点,
上的动点,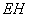 与平面
与平面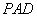 所成最大角的正切值为
所成最大角的正切值为 ,求二面角
,求二面角 的余弦值.
的余弦值.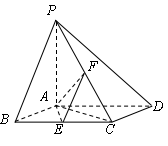
 中,已知
中,已知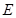 为棱
为棱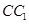 上的动点.
上的动点.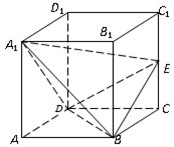
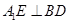 ;
;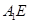 与平面
与平面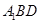 所成角的正弦值.
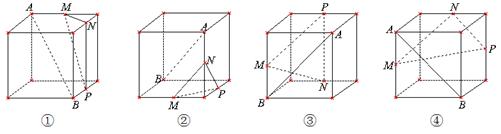
所成角的正弦值.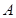 、
、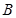 为正方体的两个顶点,
为正方体的两个顶点,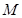 、
、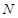 、
、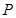 分别为其所在棱的中点,能得出
分别为其所在棱的中点,能得出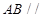 平面
平面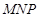 的图形的序号是( )
的图形的序号是( )