题目内容
已知多面体ABC-DEFG,AB,AC,AD两两垂直,面ABC//面DEFG,面BEF//面ADGC,AB=AD=DG=2,AC=EF=1,则该多面体的体积为( )
| A.2 | B.4 | C.6 | D.8 |
B
试题分析:取DG中点M,连接CM,AM,FM,则这个多面体的体积可以表示为棱柱BEF-ADM与三棱锥C-FMG以及四棱锥C-ABFM的和由于多面体ABC-DEFG中(如图),
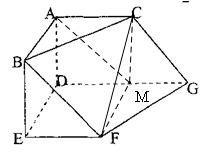
AB、AC、AD两两互相垂直,平面ABC∥平面DEFG,平面BEF∥平面ADGC,AB=AD=DG=2,AC=EF=1
故棱柱BEF-ADM可看作是底面是直角三角形的三棱锥,其高2,底面是两直角边分别是1,2的三角形其体积是2×
 ×2×1=2,三棱锥C-FMG以CM为高,其长为2,底面是MF=2,MG=1为直角边的直角三角形,其体积为
×2×1=2,三棱锥C-FMG以CM为高,其长为2,底面是MF=2,MG=1为直角边的直角三角形,其体积为 ×2×
×2× ×2×1=
×2×1=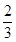 ,由图形知,C到AM的距离就是四棱锥C-ABFM的高,由于AM=
,由图形知,C到AM的距离就是四棱锥C-ABFM的高,由于AM= ,由等面积法可求得C到AM的距离是
,由等面积法可求得C到AM的距离是 ,底面四边形是以AM=
,底面四边形是以AM= 与AB=2为边长的矩形,故其体积为
与AB=2为边长的矩形,故其体积为 ×
× ×2×
×2× =
=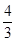 ,
,这个多面体的体积为
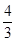 +
+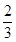 +2=4,,故选B.
+2=4,,故选B.点评:解答本题关键是根据几何体的形状对几何体进行分割,变成几个规则的几何体的体积的和,如本题转化为求棱柱,两个棱锥的体积的和.分割法是求不规则几何体的体积与面积时常用的方法.其特点是把不规则几何体的体积用几个规则的几何体的体积表示出来.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
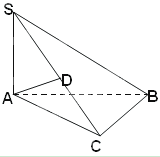
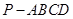 中,底面ABCD是边长为1的正方形,
中,底面ABCD是边长为1的正方形,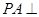 平面ABCD,PA=AB,M,N分别为PB,AC的中点,
平面ABCD,PA=AB,M,N分别为PB,AC的中点, 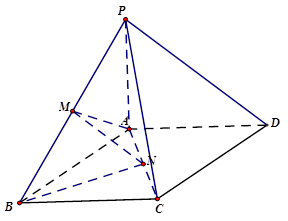
 .
.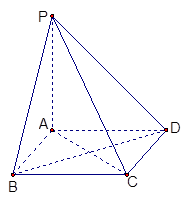
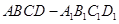 的底面边长为2,高为4,则异面直线
的底面边长为2,高为4,则异面直线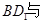
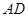 所成角的正切值是_________________.
所成角的正切值是_________________.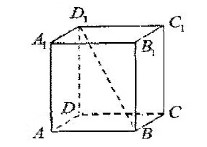
 不垂直于平面
不垂直于平面 ,那么平面
,那么平面 ,且
,且 ,过
,过 ,则
,则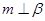
 所在的平面
所在的平面 和四边形
和四边形 所在的平面
所在的平面 互相垂直,且
互相垂直,且 ,
, ,
,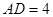 ,
, ,
, .若
.若 ,则动点
,则动点 在平面
在平面
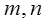 和平面
和平面 则
则 的必要非充分条件是
的必要非充分条件是 且
且
 且
且
 且
且
 与
与 成等角
成等角