题目内容
16.数列{an}满足an+1=an2-2,a1=3,求an.分析 利用3=$\frac{3+\sqrt{5}}{2}$+$\frac{3-\sqrt{5}}{2}$,写出前几项的表达式,猜想an=($\frac{3+\sqrt{5}}{2}$)2(n-1)+($\frac{3-\sqrt{5}}{2}$)2(n-1),并用数学归纳法证明即可.
解答 解:∵a1=3,
∴a1=$\frac{3+\sqrt{5}}{2}$+$\frac{3-\sqrt{5}}{2}$,
∵an+1=an2-2,
∴a2=${{a}_{1}}^{2}$-2
=($\frac{3+\sqrt{5}}{2}$+$\frac{3-\sqrt{5}}{2}$)2-2
=($\frac{3+\sqrt{5}}{2}$)2+($\frac{3-\sqrt{5}}{2}$)2,
∴a3=${{a}_{2}}^{2}$-2
=[($\frac{3+\sqrt{5}}{2}$)2+($\frac{3-\sqrt{5}}{2}$)2]2-2
=($\frac{3+\sqrt{5}}{2}$)4+($\frac{3-\sqrt{5}}{2}$)4,
猜想:an=($\frac{3+\sqrt{5}}{2}$)2(n-1)+($\frac{3-\sqrt{5}}{2}$)2(n-1).
下面用数学归纳法来证明:
①当n=1时显然成立;
②假设当n=k时,有ak=($\frac{3+\sqrt{5}}{2}$)2(k-1)+($\frac{3-\sqrt{5}}{2}$)2(k-1),
则ak+1=${{a}_{k}}^{2}$-2
=[($\frac{3+\sqrt{5}}{2}$)2(k-1)+($\frac{3-\sqrt{5}}{2}$)2(k-1)]2-2
=($\frac{3+\sqrt{5}}{2}$)2(k+1-1)+($\frac{3-\sqrt{5}}{2}$)2(k+1-1),
即当n=k+1时,结论也成立;
由①、②可知an=($\frac{3+\sqrt{5}}{2}$)2(n-1)+($\frac{3-\sqrt{5}}{2}$)2(n-1),
∴数列{an}的通项公式an=($\frac{3+\sqrt{5}}{2}$)2(n-1)+($\frac{3-\sqrt{5}}{2}$)2(n-1).
点评 本题考查数列的通项,考查数学归纳法,注意解题方法的积累,属于难题.

 小夫子全能检测系列答案
小夫子全能检测系列答案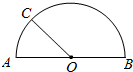 如图,在半径为1的半圆AB,O为圆心,C是半圆周上一点,设弧AC=a,则a>1的概率是$\frac{2}{3}$.
如图,在半径为1的半圆AB,O为圆心,C是半圆周上一点,设弧AC=a,则a>1的概率是$\frac{2}{3}$.