题目内容
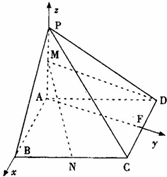
如图,在四棱锥P-ABCD中,底面ABCD是边长为1的菱形,∠ABC=
,PA⊥底面ABCD,PA=2,M为PA的中点,N为BC的中点.AF⊥CD于F,如图建立空间直角坐标系.
(Ⅰ)求出平面PCD的一个法向量并证明MN∥平面PCD;
(Ⅱ)求二面角P-CD-A的余弦值.
| π |
| 4 |
(Ⅰ)求出平面PCD的一个法向量并证明MN∥平面PCD;
(Ⅱ)求二面角P-CD-A的余弦值.

(Ⅰ)证:∵底面ABCD是边长为1的菱形,∠ABC=
,
PA⊥底面ABCD,PA=2,M为PA的中点,N为BC的中点.AF⊥CD于F,
∴由题设知:在Rt△AFD中,AF=FD=
,
∴A(0,0,0),B(1,0,0),F(0,
,0),
D(-
,
,0),P(0,0,2),M(0,0,1),N(1-
,
,0),…(4分)
∴
=(1-
,
,-1),…(5分)
=(0,
,-2),
=(-
,
,-2)…(6分)
设平面PCD的一个法向量为
=(x,y,z)
则
,∴
,
令z=
,得
=(0,4,
),
∴平面PCD的一个法向量
=(0,4,
)…(8分)
∵
•
=0+
-
=0,
∴MN∥平面PCD.…(10分)
(Ⅱ)由(Ⅰ)得平面PCD的法向量
(0,4,
),
平面ADC的一个法向量为
=(0,0,1)…(12分)
设二面角P-CD-A的平面角为α,
则cosα=
=
=
∴二面角P-CD-A的余弦值为
.…(14分)
| π |
| 4 |
PA⊥底面ABCD,PA=2,M为PA的中点,N为BC的中点.AF⊥CD于F,
∴由题设知:在Rt△AFD中,AF=FD=
| ||
| 2 |
∴A(0,0,0),B(1,0,0),F(0,
| ||
| 2 |
D(-
| ||
| 2 |
| ||
| 2 |
| ||
| 4 |
| ||
| 4 |
∴
| MN |
| ||
| 4 |
| ||
| 4 |
| PF |
| ||
| 2 |
| PD |
| ||
| 2 |
| ||
| 2 |
设平面PCD的一个法向量为
| n |
则
|
|
令z=
| 2 |
| n |
| 2 |
∴平面PCD的一个法向量
| n |
| 2 |
∵
| MN |
| n |
| 2 |
| 2 |
∴MN∥平面PCD.…(10分)
(Ⅱ)由(Ⅰ)得平面PCD的法向量
| n |
| 2 |
平面ADC的一个法向量为
| AM |
设二面角P-CD-A的平面角为α,
则cosα=
| ||||
|
|
| ||
|
| 1 |
| 3 |
∴二面角P-CD-A的余弦值为
| 1 |
| 3 |

练习册系列答案
相关题目




 =a+2b,
=a+2b, =-4a-b,
=-4a-b, =-5a-3b,其中a,b不共线,则四边形ABCD为( )
=-5a-3b,其中a,b不共线,则四边形ABCD为( )