题目内容
12.解关于x的不等式ax2-2x-2-a<0(a>-1).分析 由-1<a<0,a=0,0<a<1,a≥1,进行分类讨论,由此利用分类讨论思想和一元二次方程的解法能求出原不等式的解集.
解答 解:(1)当a=0时,有-2x-2<0,∴x>-1.
(2)a>0时,∵△=4-4a(-2-a)=4a2+8a+4=4(a+1)2>0,
方程ax2-2x-2-a=0的两根为$\frac{2±2(a+1)}{2a}$,即x1=-1,${x}_{2}=\frac{a+2}{a}$,
∴不等式的解集为{x|-1<x<$\frac{a+2}{2}$}.
(3)当-1<a<0时,△=4-4a(-2-a)=4a2+8a+4=4(a+1)2>0,
不等式ax2-2x-2-a<0的解集为{x|-1<x<$\frac{a+2}{2}$}.
综上,关于x的不等式ax2-2x-2-a<0(a>-1)的解集为:
当-1<a<0时,关于x的不等式ax2-2x-2-a<0(a>-1)的解集为:{x|-1<x<$\frac{a+2}{2}$}.
当a=0时,关于x的不等式ax2-2x-2-a<0(a>-1)的解集为:{x|x>-1};
当a>0时,关于x的不等式ax2-2x-2-a<0(a>-1)的解集为:{x|-1<x<$\frac{a+2}{2}$}.
点评 本题考查不等式的解集的求法,是中档题,解题时要认真审题,注意分类讨论思想的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20.点A(-2,m)关于点O(3,1)对称的点刚好落在直线x+y-1=0上,则m值为( )
| A. | -2 | B. | 3 | C. | 7 | D. | 9 |

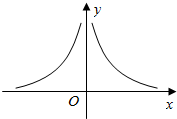 如图,幂函数y=x3m-7(m∈N)的图象关于y轴对称,且与x轴,y轴均无交点,求此函数的解析式及不等式f(x+2)<16的解集.
如图,幂函数y=x3m-7(m∈N)的图象关于y轴对称,且与x轴,y轴均无交点,求此函数的解析式及不等式f(x+2)<16的解集.