题目内容
15.求下列函数的定义域:(1)y=$\frac{1}{lg(x+1)-3}$;
(2)y=$\sqrt{lo{g}_{a}(4x-3)}$(a>0,且a≠1).
分析 (1)由分式的分母不等于0,对数式的真数大于0求解x的取值集合得答案;
(2)由根式内部的代数式大于等于0,然后对a分类求解对数不等式得答案.
解答 解:(1)由lg(x+1)-3≠0,得lg(x+1)≠3,
∴$\left\{\begin{array}{l}{x+1>0}\\{x+1≠1000}\end{array}\right.$,解得x>-1且x≠999.
∴y=$\frac{1}{lg(x+1)-3}$的定义域为(-1,999)∪(999,+∞);
(2)要使原函数有意义,则loga(4x-3)≥0.
当0<a<1时,则0<4x-3≤1,解得$\frac{3}{4}<x≤1$;
当a>1时,则4x-3≥1,解得x≥1.
当0<a<1时,函数y=$\sqrt{lo{g}_{a}(4x-3)}$的定义域为$(\frac{3}{4},1]$;
当a>1时,函数y=$\sqrt{lo{g}_{a}(4x-3)}$的定义域为[1,+∞).
点评 本题考查函数的定义域及其求法,考查了分类讨论的数学思想方法,考查对数不等式的解法,是基础题.

练习册系列答案
相关题目
16.关于x的方程$\sqrt{4-{x^2}}$=kx+2只有一个实根,则实数k的取值范围是( )
| A. | k=0 | B. | k=0或k>1 | C. | |k|>1 | D. | k=0或|k|>1 |
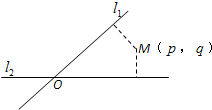 如图,平面中两条直线l1和l2相交于点O,对于平面上任意一点M,若p、q分别是M到直线l1和l2的距离,则称有序非负实数对(p,q)是点M的“距离坐标”.已知常数p≥0,q≥0,给出下列命题:
如图,平面中两条直线l1和l2相交于点O,对于平面上任意一点M,若p、q分别是M到直线l1和l2的距离,则称有序非负实数对(p,q)是点M的“距离坐标”.已知常数p≥0,q≥0,给出下列命题: