Question

6．若函数y₁=sin2x₁-$\frac{\sqrt{3}}{2}$（x₁∈[0，π]），函数y₂=x₂+3，则（x₁-x₂）²+（y₁-y₂）²的最小值为$\frac{（π+18）^{2}}{72}$．

Answer 1

分析 根据平移切线法，求出和直线y=x+3平行的切线方程和切点，利用点到直线的距离公式即可得到结论．

解答 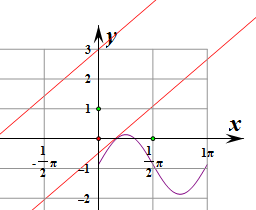解：设z=（x₁-x₂）²+（y₁-y₂）²，
则z的几何意义是两条曲线上动点之间的距离的平方，
求函数y=sin2x-$\frac{\sqrt{3}}{2}$（x∈[0，π]）的导数
f′（x）=2cos2x，
直线y=x+3的斜率k=1，
由f′（x）=2cos2x=1，即cos2x=$\frac{1}{2}$，
即2x=$\frac{π}{3}$，解得x=$\frac{π}{6}$，
此时y=sin2x-$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{2}$-$\frac{\sqrt{3}}{2}$=0，
即函数在（$\frac{π}{6}$，0）处的切线和直线y=x+3平行，
则最短距离d=$\frac{|\frac{π}{6}+3|}{\sqrt{2}}$，
∴（x₁-x₂）²+（y₁-y₂）²的最小值d²=（$\frac{|\frac{π}{6}+3|}{\sqrt{2}}$）²=$\frac{（π+18）^{2}}{72}$．
故答案为：$\frac{（π+18）^{2}}{72}$．

点评 本题主要考查导数的综合应用，利用平移切线法求直线和正弦函数距离的最小值是解决本题的关键，考查学生的运算能力．