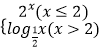Question

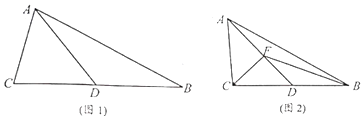
【题目】已知在多面体SP﹣ABCD中，底面ABCD为矩形，AB=PC=1，AD=AS=2，且AS∥CP且AS⊥面ABCD，E为BC的中点．

（1）求证：AE∥面SPD；

（2）求三棱锥S-BPD的体积。

Answer 1

【答案】. （1）证明见解析；（2）

【解析】试题分析：（1）要证线面平行，在题目中构造平行四边形AECQ，证得线线平行，再得线面平行。（2）根据三棱锥的体积公式，换顶点为Ｖ＝，再根据公式求出体积。

证明：（1）取SD的中点F，连接PF，过F作FQ⊥面ABCD，交AD于Q，连接QC，

∵AS⊥面ABCD，∴AS∥FQ，QF为SD的中点，∴Q为AD的中点，

FQ=AS，PC=AS，∴FQ=PC，且FQ∥PC，∴CPFQ为平行四边形，∴PF∥CQ，

又∵AQ∥∥EC，AQ=EC，∴四边形AECQ为平行四边形，∴AE∥CQ，

又PF∥CQ，∴AE∥PF，∴PF面SPD，AE面SPD，∴AE∥面SPD．

（2）设AC,BD交于点O，

Ｖ＝。