题目内容
【题目】某著名歌星在某地举办一次歌友会，有1000人参加，每人一张门票，每张100元．在演出过程中穿插抽奖活动，第一轮抽奖从这1000张票根中随机抽取10张，其持有者获得价值1000元的奖品，并参加第二轮抽奖活动．第二轮抽奖由第一轮获奖者独立操作按钮，电脑随机产生两个实数x，y（x，y∈[0，4]），若满足y≥ 
，电脑显示“中奖”，则抽奖者再次获得特等奖奖金；否则电脑显示“谢谢”，则不获得特等奖奖金．
（1）已知小明在第一轮抽奖中被抽中，求小明在第二轮抽奖中获奖的概率；
（2）设特等奖奖金为a元，小李是此次活动的顾客，求小李参加此次活动获益的期望；若该歌友会组织者在此次活动中获益的期望值是至少获得70000元，求a的最大值．
【答案】
（1）解：（Ⅰ）由题意知作图如下，
，
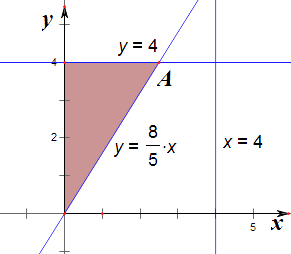结合图象可知，阴影内的面积S= 
× 
×4=5，
故小明在第二轮抽奖中获奖的概率P= 
；
（2）解：由题意，
E（X）=1000× 
+a× × =10+ 
；
故100000﹣1000×10﹣10× ×a≥70000，
即a≤6400，
故a的最大值为6400．
【解析】（1）由题意知可化为几何概率模型求解，从而作图求得；（2）易知E（X）=1000× +a× × =10+ ；100000﹣1000×10﹣10× ×a≥70000，从而再解出a的最大值．
【考点精析】关于本题考查的离散型随机变量及其分布列，需要了解在射击、产品检验等例子中，对于随机变量X可能取的值，我们可以按一定次序一一列出，这样的随机变量叫做离散型随机变量．离散型随机变量的分布列：一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn，X取每一个值 xi(i=1,2,......）的概率P(ξ=xi）＝Pi，则称表为离散型随机变量X 的概率分布，简称分布列才能得出正确答案．
