题目内容
3.斜率为k(k>0)的直线l与抛物线C:y2=4x交于A,B两点,O为原点,M是线段AB的中点,F为C的焦点,△OFM的面积等于2,则k=$\frac{1}{2}$.分析 利用△OFM的面积等于2,求出M的纵坐标,设直线l的方程为x=my+b,代入y2=4x可得y2-4my-4b=0,利用韦达定理,求出m,即可求出k的值.
解答 解:设M(x,y)(y>0),则
由抛物线C:y2=4x,可得F(1,0),
∵△OFM的面积等于2,
∴$\frac{1}{2}•1•|y|$=2,
∴y=4,
设直线l的方程为x=my+b,代入y2=4x可得y2-4my-4b=0,
设A(x1,y1)、B(x2,y2),则y1+y2=4m,
∴2m=4,
∴m=2,
∴k=$\frac{1}{m}$=$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 本题考查直线与抛物线的位置关系,考查三角形面积的计算,考查韦达定理的运用,属于中档题.

练习册系列答案
相关题目
11.等差数列{an}中,a1<0,Sn为第n项,且S3=S16,则Sn取最小值时,n的值( )
| A. | 9 | B. | 10 | C. | 9或10 | D. | 10或11 |
15.若函数f(x)=1ogax(0<a<1)在区间[a,3a]上的最大值是最小值的2倍,则a=( )
| A. | $\frac{2}{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{9}$ |
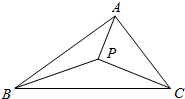 如图所示,点P在已知三角形ABC的内部,定义有序实数对(μ,v,ω) 为点P关于△ABC的面积坐标,其中μ=$\frac{△PBC的面积}{△ABC的面积}$,v=$\frac{△APC的面积}{△ABC的面积}$,ω=$\frac{△ABP的面积}{△ABC的面积}$;若点Q满足$\overrightarrow{BQ}$=$\frac{1}{3}$$\overrightarrow{BC}$+$\frac{1}{2}$$\overrightarrow{BA}$,则点Q关于△ABC的面积坐标($\frac{1}{2}$,$\frac{1}{6}$,$\frac{1}{3}$).
如图所示,点P在已知三角形ABC的内部,定义有序实数对(μ,v,ω) 为点P关于△ABC的面积坐标,其中μ=$\frac{△PBC的面积}{△ABC的面积}$,v=$\frac{△APC的面积}{△ABC的面积}$,ω=$\frac{△ABP的面积}{△ABC的面积}$;若点Q满足$\overrightarrow{BQ}$=$\frac{1}{3}$$\overrightarrow{BC}$+$\frac{1}{2}$$\overrightarrow{BA}$,则点Q关于△ABC的面积坐标($\frac{1}{2}$,$\frac{1}{6}$,$\frac{1}{3}$).