题目内容
18．已知曲线y=$\frac{a}{{e}^{x}+1}$（其中e为自然对数的底数）在x=0处的切线的倾斜角为135°，则实数a的值是4．分析 求出函数的导数，求得切线的斜率，由直线的斜率公式，计算即可得到所求值．
解答 解：y=$\frac{a}{{e}^{x}+1}$的导数为y′=-$\frac{a{e}^{x}}{（{e}^{x}+1）^{2}}$，
在x=0处的切线的倾斜角为135°，
即有k=-$\frac{a}{4}$=-1，
解得a=4．
故答案为：4．
点评 本题考查导数的运用：求切线的斜率，考查直线的斜率公式的运用，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
8．已知a，b是实数，命题p：“a+b＞5”，命题q：“$\left\{\begin{array}{l}{a＞2}\\{b＞3}\end{array}\right.$”，则￢p是￢q的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充分必要条件 | D． | 既不充分也不必要条件 |
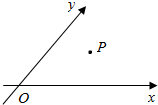如图，设α∈（0，π）且$α≠\frac{π}{2}$，当∠xOy=α时，定义平面坐标系xOy为斜坐标系，在斜坐标系中，任意一点P的斜坐标这样定义：e1，e2分别为x轴、y轴正方向相同的单位向量，若$\overrightarrow{OP}=x{e_1}+y{e_2}$，则记为$\overrightarrow{OP}=（x，y）$，那么在以下的结论中，正确的有（2）（4）（填上所有正确结论的序号）．