题目内容
8.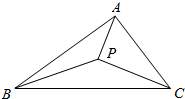 如图所示,点P在已知三角形ABC的内部,定义有序实数对(μ,v,ω) 为点P关于△ABC的面积坐标,其中μ=$\frac{△PBC的面积}{△ABC的面积}$,v=$\frac{△APC的面积}{△ABC的面积}$,ω=$\frac{△ABP的面积}{△ABC的面积}$;若点Q满足$\overrightarrow{BQ}$=$\frac{1}{3}$$\overrightarrow{BC}$+$\frac{1}{2}$$\overrightarrow{BA}$,则点Q关于△ABC的面积坐标($\frac{1}{2}$,$\frac{1}{6}$,$\frac{1}{3}$).
如图所示,点P在已知三角形ABC的内部,定义有序实数对(μ,v,ω) 为点P关于△ABC的面积坐标,其中μ=$\frac{△PBC的面积}{△ABC的面积}$,v=$\frac{△APC的面积}{△ABC的面积}$,ω=$\frac{△ABP的面积}{△ABC的面积}$;若点Q满足$\overrightarrow{BQ}$=$\frac{1}{3}$$\overrightarrow{BC}$+$\frac{1}{2}$$\overrightarrow{BA}$,则点Q关于△ABC的面积坐标($\frac{1}{2}$,$\frac{1}{6}$,$\frac{1}{3}$).
分析 可作出图形,然后作QD∥BC,QE∥AB,分别交AB,BC于D,E,从而根据向量加法的平行四边形法则知$\overrightarrow{BD}=\frac{1}{2}\overrightarrow{BA},\overrightarrow{BE}=\frac{1}{3}\overrightarrow{BC}$,从而得到$DQ=\frac{1}{3}BC,QE=\frac{1}{2}BA$,这样根据三角形的面积公式即可得出${S}_{△ABQ}=\frac{1}{3}{S}_{△ABC}$,${S}_{△QBC}=\frac{1}{2}{S}_{△ABC}$,这样即可求出μ,v,ω,从而得出点Q关于△ABC的面积的坐标.
解答  解:如图,过Q作QD∥BC,交AB于D,作QE∥AB,交BC于E,则:
解:如图,过Q作QD∥BC,交AB于D,作QE∥AB,交BC于E,则:
$DQ=\frac{1}{3}BC,QE=\frac{1}{2}AB$;
∴$μ=\frac{{S}_{△QBC}}{{S}_{△ABC}}=\frac{1}{2},ω=\frac{{S}_{△ABQ}}{{S}_{△ABC}}=\frac{1}{3}$;
∴$v=1-\frac{1}{2}-\frac{1}{3}=\frac{1}{6}$;
∴点Q关于△ABC的面积坐标为($\frac{1}{2},\frac{1}{6},\frac{1}{3}$).
故答案为:$(\frac{1}{2},\frac{1}{6},\frac{1}{3})$.
点评 考查向量加法的平行四边形法则,共线向量基本定理,向量数乘的几何意义,以及三角形的面积公式.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
16.如果将函数f(x)=2sin3x的图象向左平移$\frac{φ}{3}(φ>0)$个单位长度,得到函数g(x)的图象,若g(x)的图象关于直线$x=\frac{π}{4}$对称,则φ的最小值是( )
| A. | $\frac{3π}{4}$ | B. | $\frac{π}{2}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{6}$ |