题目内容
【题目】已知函数![]() ,
, ![]() (
(![]() 为自然对数的底数).
为自然对数的底数).
(1)设曲线![]() 在
在![]() 处的切线为
处的切线为![]() ,若
,若![]() 与点
与点![]() 的距离为
的距离为![]() ,求
,求![]() 的值;
的值;
(2)若对于任意实数![]() ,
, ![]() 恒成立,试确定
恒成立,试确定![]() 的取值范围;
的取值范围;
(3)当![]() 时,函数
时,函数![]() 在
在![]() 上是否存在极值?若存在,请求出极值;若不存在,请说明理由.
上是否存在极值?若存在,请求出极值;若不存在,请说明理由.
【答案】(1) ![]() 或
或![]() (2)
(2) ![]() (3)不存在
(3)不存在
【解析】试题分析:
(1)该问切点横坐标已知,则利用切点在曲线上,带入曲线![]() 即可得到切点的纵坐标,对
即可得到切点的纵坐标,对![]() 进行求导并得到在切点处的导函数值即为切线的斜率,有切线的斜率,切线又过切点,利用直线的点斜式即可求的切线的方程,利用点到直线的距离公式结合条件点
进行求导并得到在切点处的导函数值即为切线的斜率,有切线的斜率,切线又过切点,利用直线的点斜式即可求的切线的方程,利用点到直线的距离公式结合条件点![]() 到切线的距离为
到切线的距离为![]() 即可求的参数
即可求的参数![]() 的值.
的值.
(2)该问为恒成立问题可以考虑分离参数法,即把参数a与x进行分离得到![]() ,则
,则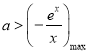 ,再利用函数的导函数研究函数
,再利用函数的导函数研究函数![]() 在区间
在区间![]() 的最大值,即可求的a的取值范围.
的最大值,即可求的a的取值范围.
(3)根据极值的定义,函数![]() 在区间
在区间![]() 有零点且在零点附近的符号不同,求导可得
有零点且在零点附近的符号不同,求导可得![]() ,设
,设![]() ,求
,求![]() 求导可以得到
求导可以得到![]() 的导函数在区间
的导函数在区间![]() 恒为正数,则函数
恒为正数,则函数![]() 在区间
在区间![]() 上是单调递增,即可得到函数
上是单调递增,即可得到函数![]() 进而得到
进而得到![]() 恒成立,即
恒成立,即![]() 在区间
在区间![]() 上没有零点,进而函数
上没有零点,进而函数![]() 没有极值.
没有极值.
试题解析:
(1)![]() ,
, ![]() .
.
![]() 在
在![]() 处的切线斜率为
处的切线斜率为![]() , 1分
, 1分
∴切线![]() 的方程为
的方程为![]() ,即
,即![]() . 3分
. 3分
又切线![]() 与点
与点![]() 距离为
距离为![]() ,所以
,所以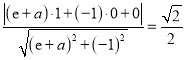 ,
,
解之得, ![]() 或
或![]() 5分
5分
(2)∵对于任意实数![]() 恒成立,
恒成立,
∴若![]() ,则
,则![]() 为任意实数时,
为任意实数时, ![]() 恒成立; 6分
恒成立; 6分
若![]()
![]() 恒成立,即
恒成立,即![]() ,在
,在![]() 上恒成立, 7分
上恒成立, 7分
设![]() 则
则![]() , 8分
, 8分
当![]() 时,
时, ![]() ,则
,则![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,
时, ![]() ,则
,则![]() 在
在![]() 上单调递减;
上单调递减;
所以当![]() 时,
时, ![]() 取得最大值,
取得最大值, ![]() , 9分
, 9分
所以![]() 的取值范围为
的取值范围为![]() .
.
综上,对于任意实数![]() 恒成立的实数
恒成立的实数![]() 的取值范围为
的取值范围为![]() . 10分
. 10分
(3)依题意, ![]() ,
,
所以![]() , 2分
, 2分
设![]() ,则
,则![]() ,当
,当![]() ,
,
故![]() 在
在![]() 上单调增函数,因此
上单调增函数,因此![]() 在
在![]() 上的最小值为
上的最小值为![]() ,
,
即![]() , 12分
, 12分
又![]() 所以在
所以在![]() 上,
上, ![]() ,
,
即![]() 在
在![]() 上不存在极值. 14分
上不存在极值. 14分

 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案【题目】某企业为了对生产的一种新产品进行合理定价,将该产品按事先拟定的价格进行试销,得到以下数据:
单价x(元/件) | 60 | 62 | 64 | 66 | 68 | 70 |
销量y(件) | 91 | 84 | 81 | 75 | 70 | 67 |
(I)画出散点图,并求![]() 关于
关于![]() 的回归方程;
的回归方程;
(II)已知该产品的成本是36元/件,预计在今后的销售中,销量与单价仍然服从(I)中的关系,为使企业获得最大利润,该产品的单价应定为多少元(精确到元)?
附:回归直线![]() 的斜率和截距的最小二乘法估计公式分别为:
的斜率和截距的最小二乘法估计公式分别为:
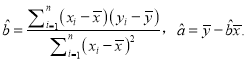
【题目】全世界越来越关注环境保护问题,某监测站点于2016年8月某日起连续![]() 天监测空气质量指数
天监测空气质量指数![]() ,数据统计如下:
,数据统计如下:
空气质量指数 |
|
|
|
|
|
空气质量等级 | 空气优 | 空气良 | 轻度污染 | 中度污染 | 重度污染 |
天数 |
|
|
|
|
|
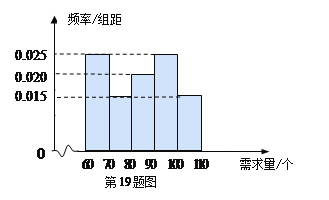
(1)根据所给统计表和频率分布直方图中的信息求出![]() 的值,并完成頻率分布直方图:
的值,并完成頻率分布直方图:
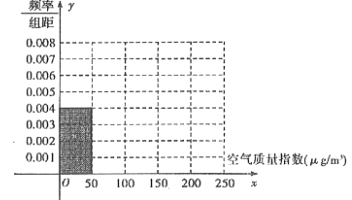
(2)由頻率分布直方图,求该组数据的平均数与中位数;
(3)在空气质量指数分别为![]() 和
和![]() 的监测数据中,用分层抽样的方法抽取
的监测数据中,用分层抽样的方法抽取![]() 天,从中任意选取
天,从中任意选取![]() 天,求事件
天,求事件![]() “两天空气都为良”发生的概率.
“两天空气都为良”发生的概率.