题目内容
(本小题满分14分)设椭圆的中心是坐标原点,长轴在x轴上,离心率e=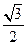 ,已知点P(0,
,已知点P(0,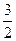 )到这个椭圆上的点的最远距离是
)到这个椭圆上的点的最远距离是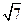 ,求这个椭圆的方程。
,求这个椭圆的方程。
解:由题设e=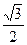 可得a2=4b2,于是,设椭圆方程为
可得a2=4b2,于是,设椭圆方程为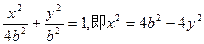 …………4分
…………4分
又设M(x,y)是椭圆上任意一点,且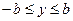 ,
,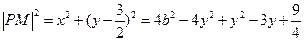
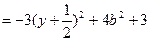 ………9分
………9分
因为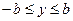 ,所以
,所以
①若b<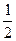 ,当y=-b时,
,当y=-b时,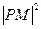 有最大值为
有最大值为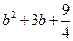 =
=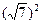
解得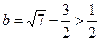 与b<
与b<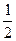 相矛盾(即不合题意).……11分
相矛盾(即不合题意).……11分
②若b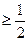 ,当y=-
,当y=-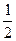 时,
时,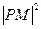 有最大值为
有最大值为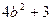 =
=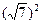
解得 b=1,a=2.……13分
故所求椭圆方程为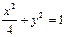 .…14分
.…14分
解析

练习册系列答案
相关题目
已知椭圆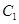 ,抛物线
,抛物线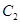 的焦点均在
的焦点均在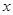 轴上,
轴上,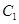 的中心和
的中心和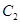 的顶点均为坐标原点
的顶点均为坐标原点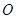 ,从每条曲线上各取两个点,将其坐标记录于表中:
,从每条曲线上各取两个点,将其坐标记录于表中:
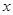 | 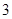 | 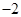 |  | 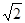 |
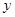 | 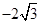 |  | 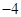 | 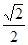 |
(1)求
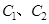 的标准方程;
的标准方程;(2)请问是否存在直线
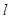 同时满足条件:(ⅰ)过
同时满足条件:(ⅰ)过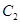 的焦点
的焦点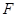 ;(ⅱ)与
;(ⅱ)与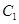 交于不同两点
交于不同两点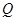 、
、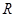 ,且满足
,且满足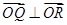 .若存在,求出直线
.若存在,求出直线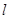 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由. 在极坐标系中,圆ρ=2cos θ的垂直于极轴的两条切线方程分别为( )
| A.θ=0(ρ∈R)和ρcos θ=2 | B.θ=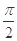 (ρ∈R)和ρcos θ=2 (ρ∈R)和ρcos θ=2 |
C.θ=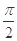 (ρ∈R)和ρcos θ=1 (ρ∈R)和ρcos θ=1 | D.θ=0(ρ∈R)和ρcos θ=1 |
 的两个焦点分别为
的两个焦点分别为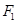 、
、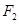 ,离心率为2.
,离心率为2.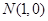 能否作出直线
能否作出直线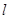 ,使
,使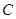 交于
交于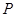 、
、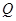 两点,且
两点,且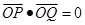 ,若存在,求出直线方程,若不存在,说明理由.
,若存在,求出直线方程,若不存在,说明理由.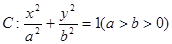 经过点
经过点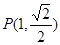 ,且两焦点与短轴的一个端点的连线构成等腰直角三角形.
,且两焦点与短轴的一个端点的连线构成等腰直角三角形.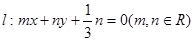 交椭圆C于A、B两点,试问:在坐标平面上是否存在一个定点T,使得以AB为直径的圆恒过点T。若存在,求出点T的坐标;若不存在,请说明理由.
交椭圆C于A、B两点,试问:在坐标平面上是否存在一个定点T,使得以AB为直径的圆恒过点T。若存在,求出点T的坐标;若不存在,请说明理由.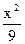 +
+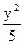 =1的焦点F1、F2,在直线l:x+y-6=0上找一点M,求以F1、F2为焦点,通过点M且长轴最短的椭圆方程.
=1的焦点F1、F2,在直线l:x+y-6=0上找一点M,求以F1、F2为焦点,通过点M且长轴最短的椭圆方程.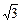 ,求椭圆的方程.
,求椭圆的方程. 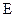 的中心是坐标原点,焦点在坐标轴上,且椭圆过点
的中心是坐标原点,焦点在坐标轴上,且椭圆过点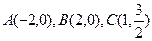 三点.
三点.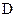 为椭圆
为椭圆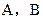 的任意一点,
的任意一点,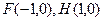 ,求
,求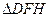 内切圆的面积的最大值,并指出其内切圆圆心的坐标.
内切圆的面积的最大值,并指出其内切圆圆心的坐标.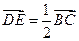 ,求以B,C为焦点且过点D,E的双曲线的离心
,求以B,C为焦点且过点D,E的双曲线的离心