题目内容
【题目】地为绿化环境，移栽了银杏树
棵，梧桐树
棵.它们移栽后的成活率分别
为
、
，每棵树是否存活互不影响，在移栽的
棵树中：
（1）求银杏树都成活且梧桐树成活
棵的概率；
（2）求成活的棵树
的分布列与期望.
【答案】（1）
；（2）详见解析.
【解析】
试题分析：（1）先求出银杏数分别成活
、
、
棵的概率，以及梧桐树分别成活
、
、
、
棵的概率，
然后利用事件的独立性求出题中事件的概率；（2）先确定随机变量
的可能取值，利用事件的独立性求出
随机变量
在相应取值下的概率，列出分布列求出随机变量的数学期望即可.
（1）设
表示“银杏树都成活且梧桐树成活
棵”，
设
表示“银杏树成活
棵”；
，
，
，
表示“梧桐树成活
棵”；
，
，
，
，
；
（2）
的可能的取值：
、
、
、
、
、
，
，
，
，
同理：
，
，
，
的分布列为
|
|
|
|
|
|
|
|
|
|
|
|
|
|
.
【题目】某地随着经济的发展，居民收入逐年增长，下表是该地一建设银行连续五年的储蓄存款（年底余额），如下表1：
年份x | 2011 | 2012 | 2013 | 2014 | 2015 |
储蓄存款y（千亿元） | 5 | 6 | 7 | 8 | 10 |
为了研究计算的方便，工作人员将上表的数据进行了处理， 
得到下表2：
时间代号t | 1 | 2 | 3 | 4 | 5 |
z | 0 | 1 | 2 | 3 | 5 |
（Ⅰ）求z关于t的线性回归方程；
（Ⅱ）通过（Ⅰ）中的方程，求出y关于x的回归方程；
（Ⅲ）用所求回归方程预测到2020年年底，该地储蓄存款额可达多少？
（附：对于线性回归方程
，其中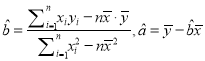
）
【题目】设圆
的圆心为
，直线
过点
且与
轴不重合， 
交圆
于
两点，过
作
的平行线交
于点
.
（1）证明
为定值，并写出点
的轨迹方程；
（2）设
，过点
作直线
，交点
的轨迹于
两点 (异于
),直线
的斜率分别为
，证明： 
为定值.
【题目】“累积净化量（
）”是空气净化器质量的一个重要衡量指标，它是指空气净化器从开始使用到净化效率为
时对颗粒物的累积净化量，以克表示.根据
《空气净化器》国家标准，对空气净化器的累计净化量（
）有如下等级划分：
累积净化量（克） |
|
|
| 12以上 |
等级 |
|
|
|
|
为了了解一批空气净化器（共2000台）的质量，随机抽取
台机器作为样本进行估计，已知这
台机器的累积净化量都分布在区间
中.按照
均匀分组，其中累积净化量在
的所有数据有： 
和
，并绘制了如下频率分布直方图：
（1）求
的值及频率分布直方图中的
值；
（2）以样本估计总体，试估计这批空气净化器（共2000台）中等级为
的空气净化器有多少台？
（3）从累积净化量在
的样本中随机抽取2台，求恰好有1台等级为
的概率.
