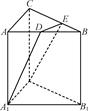
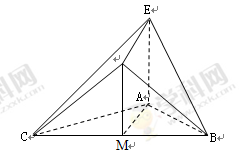
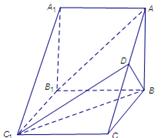
题目内容
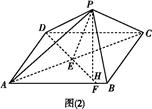
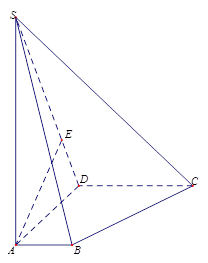
在如图所示的几何体中, 是边长为
是边长为 的正三角形,
的正三角形, ,
, 平面
平面 ,平面
,平面 平面
平面 ,
,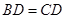 ,且
,且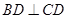 .
.
(1)证明: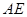 //平面
//平面 ;
;
(2)证明:平面 平面
平面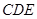 ;
;
(3)求该几何体的体积.
(1)详见解析;(2)详见解析;(3)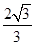
解析试题分析:(1)取 的中点
的中点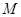 ,根据等腰三角形中线即为高线可得
,根据等腰三角形中线即为高线可得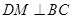 ,又因为面
,又因为面 平面
平面 ,根据面面垂直的性质定理可得
,根据面面垂直的性质定理可得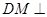 平面
平面 ,已知
,已知 平面
平面 ,所以
,所以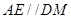 ,根据线面平行的判定定理可得
,根据线面平行的判定定理可得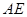 //平面
//平面 。(2)因为
。(2)因为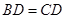 ,且
,且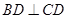 ,斜边中线
,斜边中线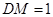 ,又因为
,又因为 ,
,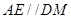 可证得
可证得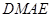 是平行四边形,可得
是平行四边形,可得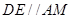 ,根据线面垂直的判定定理可证得
,根据线面垂直的判定定理可证得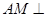 平面
平面 ,即
,即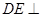 平面
平面 ,从而可得
,从而可得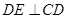 ,又因为
,又因为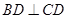 即可证得
即可证得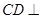 平面
平面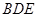 ,从而证得平面
,从而证得平面 平面
平面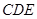 。(3)根据前两问的条件可证得
。(3)根据前两问的条件可证得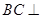 平面
平面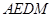 ,从而可将此几何体分割为以四边形
,从而可将此几何体分割为以四边形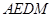 为底面的两个四棱锥,然后再求其体积。
为底面的两个四棱锥,然后再求其体积。
试题解析:证明:
(1) 取 的中点
的中点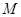 ,连接
,连接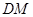 、
、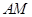 ,
,
由已知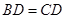 ,可得:
,可得: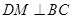 ,
,
又因为平面 ⊥平面
⊥平面 ,平面
,平面
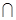 平面
平面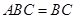 ,
,
所以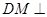 平面
平面 ,
,
因为 平面
平面 , 所以
, 所以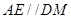 ,
,
又因为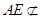 平面
平面 ,
,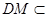 平面
平面 ,
,
所以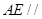 平面
平面 . 4分
. 4分
(2)由(1)知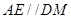 ,又
,又 ,
,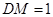 ,
,
所以四边形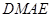 是平行四边形,则有
是平行四边形,则有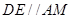 ,
,
由(1)得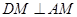 ,又
,又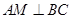 ,
,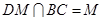
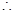
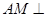 平面
平面 , 所以
, 所以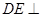 平面
平面 ,
,
又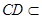

练习册系列答案
相关题目

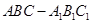 中,侧棱
中,侧棱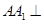 底面
底面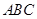 ,
, 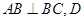 为
为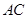 的中点,
的中点,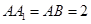 .
.
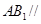 平面
平面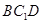 ;
; ,求三棱锥
,求三棱锥 的体积.
的体积. AC
AC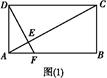
 ABC体积的最大值.
ABC体积的最大值.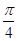 ,∠DAB=
,∠DAB=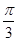 .沿直径AB折起,使两个半圆所在的平面互相垂直(如图乙),F为BC的中点,E为AO的中点.根据图乙解答下列各题:
.沿直径AB折起,使两个半圆所在的平面互相垂直(如图乙),F为BC的中点,E为AO的中点.根据图乙解答下列各题: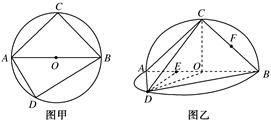
 上是否存在一点G,使得FG∥平面ACD?若存在,试确定点G的位置;若不存在,请说明理由.
上是否存在一点G,使得FG∥平面ACD?若存在,试确定点G的位置;若不存在,请说明理由. 底面ABCD,且SA=2,AD=DC=1, 点E在SD上,且
底面ABCD,且SA=2,AD=DC=1, 点E在SD上,且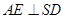
 平面
平面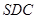 ;
;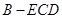 的体积
的体积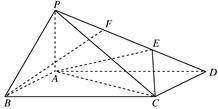
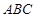 中,
中,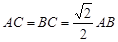 ,
, 是边长为
是边长为 的正方形,平面
的正方形,平面 、
、 分别是
分别是 、
、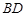 的中点.
的中点.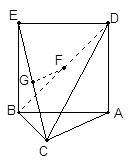
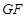 ∥底面
∥底面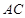 ⊥平面
⊥平面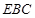 ;
;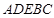 的体积.
的体积.