题目内容
圆在 ,
,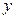 轴上分别截得弦长为
轴上分别截得弦长为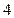 和
和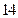 ,且圆心在直线
,且圆心在直线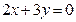 上,求此圆方程.
上,求此圆方程.
 ,
,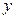 轴上分别截得弦长为
轴上分别截得弦长为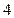 和
和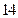 ,且圆心在直线
,且圆心在直线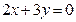 上,求此圆方程.
上,求此圆方程.圆的方程为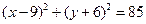 或
或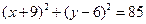
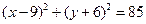 或
或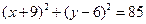
设圆的圆心为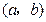 ,圆的半径为
,圆的半径为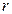 ,
,
则圆的方程为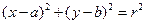 .
.
 圆在
圆在 轴,
轴,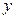 轴上截得的弦长分别为
轴上截得的弦长分别为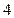 和
和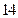 .则有
.则有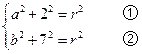
又 圆心在直线
圆心在直线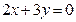 上,
上,

由①②③可得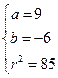 ,或
,或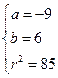
 适合题意的圆的方程为
适合题意的圆的方程为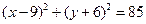 或
或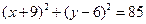 .
.
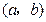 ,圆的半径为
,圆的半径为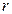 ,
,则圆的方程为
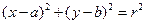 .
. 圆在
圆在 轴,
轴,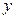 轴上截得的弦长分别为
轴上截得的弦长分别为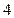 和
和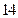 .则有
.则有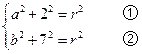
又
 圆心在直线
圆心在直线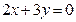 上,
上,
由①②③可得
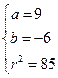 ,或
,或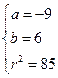
 适合题意的圆的方程为
适合题意的圆的方程为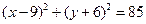 或
或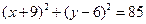 .
.
练习册系列答案
 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案
相关题目
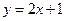 上,且到
上,且到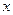 轴的距离恰等于圆的半径,在
轴的距离恰等于圆的半径,在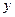 轴上截得的弦长为
轴上截得的弦长为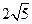 ,求此圆的方程.
,求此圆的方程.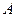 和
和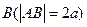 在平面内转动,并且转动时两杆保持交角为45度,求两杆交点
在平面内转动,并且转动时两杆保持交角为45度,求两杆交点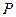 的轨迹.
的轨迹.
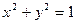 上任意一点,∠AOP的平分线交PA于M(O为原点),试求点M的轨迹.
上任意一点,∠AOP的平分线交PA于M(O为原点),试求点M的轨迹.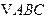 中,若两点
中,若两点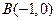 、
、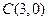 ,
,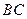 边中线
边中线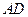 的长度为4,则点A的轨迹方程为( )
的长度为4,则点A的轨迹方程为( )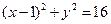
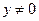 )
)
 )
)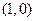 ,且总与直线
,且总与直线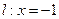 相切.
相切.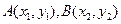 两点,当
两点,当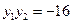 时,
时,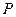 是
是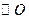 外一点,
外一点,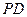 为
为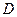 为
为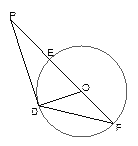 切点,割线PEF经过圆心
切点,割线PEF经过圆心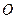 ,若
,若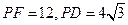 ,则
,则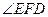 的度数为 .
的度数为 .