题目内容
已知△ABC中,∠ABC=90°,BC=3,AC=4,P是AB上的点,求点P到AC、BC的距离乘积的最大值.
∵∠ABC=90°,BC=3,AC=4,P是AB上的点,依题意,作图如下:
BC在x轴上,B点与原点O重合,点A(0,b)在y轴正半轴上,
依题意知,b=
=
,
设点P(0,m)(0<m<
),
∵直线AC的方程为
+
=1,即
x+3y-3
=0,
∴点P(0,m)到直线
x+3y-3
=0的距离(即点P(0,m)到AC的距离)d=
=
|m-
|=
(
-m),
又点P(0,m)到BC的距离为m,
∴点P到AC、BC的距离乘积f(m)=m•
(
-m)≤
•(
)2=
•
=
(当且仅当m=
时取“=”).
∴点P到AC、BC的距离乘积的最大值为
.
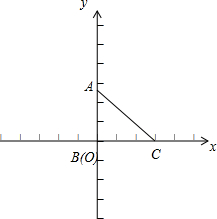
BC在x轴上,B点与原点O重合,点A(0,b)在y轴正半轴上,
依题意知,b=
| 42-32 |
| 7 |
设点P(0,m)(0<m<
| 7 |
∵直线AC的方程为
| x |
| 3 |
| y | ||
|
| 7 |
| 7 |
∴点P(0,m)到直线
| 7 |
| 7 |
|3m-3
| ||||
|
| 3 |
| 4 |
| 7 |
| 3 |
| 4 |
| 7 |
又点P(0,m)到BC的距离为m,
∴点P到AC、BC的距离乘积f(m)=m•
| 3 |
| 4 |
| 7 |
| 3 |
| 4 |
m+(
| ||
| 2 |
| 3 |
| 4 |
| 7 |
| 4 |
| 21 |
| 16 |
| ||
| 2 |
∴点P到AC、BC的距离乘积的最大值为
| 21 |
| 16 |


练习册系列答案
相关题目
 的直径
的直径 的长为4,点
的长为4,点 平分弧
平分弧 ,过
,过 ,交
,交 .
. :
: 的角平分线,求
的角平分线,求 的长.
的长.
 ,则它的边与半径为
,则它的边与半径为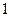 的圆的公共点个数最多为( )
的圆的公共点个数最多为( )



 平分圆
平分圆 ,则
,则 的最小值是
的最小值是
 做圆的切线切于
做圆的切线切于 点,作割线交圆于
点,作割线交圆于 两点,其中
两点,其中
 ,则
,则 .
.