题目内容
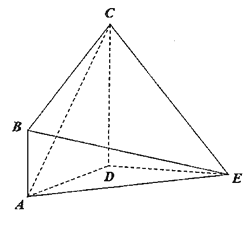
【题目】如图所示，在四棱锥
中，
平面
，
，
，
.
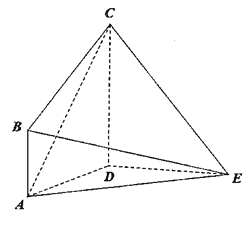
（1）求证：
；
（2）当几何体
的体积等于
时，求四棱锥的侧面积.
【答案】（1）证明见解析；（2）
.
【解析】
（1）连结BD，取CD的中点F，连结BF，证明BC⊥BD，BC⊥DE，即可证明BC⊥平面
BDE，推出BC⊥BE．（2）利用体积求出DE=2，然后求解EA，通过就是BE2=AB2+AE2，
证明AB⊥AE，然后求解四棱锥E﹣ABCD的侧面积．
（1）连结BD，取CD的中点F，连结BF，则直角梯形ABCD中，BF⊥CD，BF=CF=DF，
∴∠CBD=90°即：BC⊥BD
∵DE⊥平面ABCD，BC平面ABCD∴BC⊥DE
又BD∩DE=D∴BC⊥平面BDE
由BE平面BDE得：BC⊥BE
（2）∵
，
∴DE=2
∴
，
，
又AB=2，∴BE2=AB2+AE2
∴AB⊥AE
∴四棱锥E﹣ABCD的侧面积为
练习册系列答案
中考解读考点精练系列答案
各地期末复习特训卷系列答案
相关题目
