题目内容
20.已知函数f(x)=$\frac{1}{2}$x2-alnx(a>0)(I)求f(x)的单调区间
(Ⅱ)求f(x)在区间[1,e]上的最小值;
(Ⅲ)若f(x)在区间(1,e)上恰有两个零点,求a的取值范围.
分析 (Ⅰ)先求出函数的导数,解关于导函数的不等式,从而求出函数的单调区间;
(Ⅱ)可得x=$\sqrt{a}$为函数的临界点,通过讨论a的范围,结合函数的单调性,可得最值;
(Ⅲ)由(Ⅱ)可知当0<a≤1或a≥e2时,不合题意,当1<a<e2时,得到不等式组,解之可得a的范围.
解答 解:(Ⅰ)f′(x)=x-$\frac{a}{x}$=$\frac{{x}^{2}-a}{x}$,
令f′(x)>0,解得:x>$\sqrt{a}$,令f′(x)<0,解得:0<x<$\sqrt{a}$,
∴函数f(x)在(0,$\sqrt{a}$)递减,在($\sqrt{a}$,+∞)递增;
(Ⅱ)①若 $\sqrt{a}$≤1,即0<a≤1,在(1,e)上,f′(x)>0,f(x)在[1,e]上单调递增,
因此,f(x)在区间[1,e]的最小值为f(1)=$\frac{1}{2}$.
②若1<$\sqrt{a}$<e,即1<a<e2,在(1,$\sqrt{a}$)上,f′(x)<0,f(x)单调递减;
在($\sqrt{a}$,e)上,f′(x)>0,f(x)单调递增,因此f(x)在区间[1,e]上的最小值为f($\sqrt{a}$)=$\frac{1}{2}$a(1-lna),
③若$\sqrt{a}$≥e,即a≥e2在(1,e上,f′(x)<0,f(x)在[1,e]上单调递减,
因此,f(x)在区间[1,e]上的最小值为f(e)=$\frac{1}{2}$e2-a.
综上,当0<a≤1时,fmin(x)=$\frac{1}{2}$;
当1<a<e2时,fmin(x)=$\frac{1}{2}$a(1-lna);
当a≥e2时,fmin(x)=$\frac{1}{2}$e2-a.
(Ⅲ) 由(Ⅱ)可知当0<a≤1或a≥e2时,
f(x)在(1,e)上是单调递增或递减函数,不可能存在两个零点,
当1<a<e2时,要使f(x)在区间(1,e)上恰有两个零点,
则$\left\{\begin{array}{l}{\frac{1}{2}a(1-lna)<0}\\{f(1)=\frac{1}{2}>0}\\{f(e)={\frac{1}{2}e}^{2}-a>0}\end{array}\right.$,解得:e<a<$\frac{1}{2}$e2,
∴a的取值范围为(e,$\frac{1}{2}$e2).
点评 本题考查利用导数研究函数的切线,涉及函数的零点和闭区间的最值,属中档题.

| A. | 90 | B. | 121 | C. | 119 | D. | 120 |
| A. | 4 | B. | 2 | C. | 16-4$\sqrt{3}$ | D. | 10 |
| A. | $\frac{\sqrt{5}}{5}$ | B. | $\frac{2\sqrt{5}}{5}$ | C. | -$\frac{\sqrt{5}}{5}$ | D. | -$\frac{2\sqrt{5}}{5}$ |
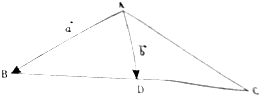 如图,在△ABC中,D为BC中点,记$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,已知|$\overrightarrow{a}$|=2,|$\overrightarrow{b}$|=1,<$\overrightarrow{a}$,$\overrightarrow{b}$>=$\frac{π}{3}$.
如图,在△ABC中,D为BC中点,记$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,已知|$\overrightarrow{a}$|=2,|$\overrightarrow{b}$|=1,<$\overrightarrow{a}$,$\overrightarrow{b}$>=$\frac{π}{3}$.