题目内容
18.已知函数f(x)在区间[0,+∞)上单调递增,且对任意的实数a∈R有f(-a)+f(a)=0恒成立.(1)判断f(x)在(-∞,0]上的单调性,并证明;
(2)求适合不等式f(2x-1)<f($\frac{1}{3}$)的x的取值范围.
分析 (1)函数f(x)在(-∞,0]上单调递增.运用单调性的定义和f(x)为奇函数的性质,即可得证;
(2)由(1)可得,f(x)在R上单调递增,不等式f(2x-1)<f($\frac{1}{3}$)即为2x-1<$\frac{1}{3}$,进而得到所求范围.
解答 解:(1)函数f(x)在(-∞,0]上单调递增.
理由:设x1,x2∈(-∞,0],且x1<x2,
则-x1,-x2∈[0,+∞),且-x1>-x2,
由函数f(x)在区间[0,+∞)上单调递增,
即有f(-x1)>f(-x2),
又对任意的实数a∈R有f(-a)+f(a)=0恒成立,
则有f(-x1)=-f(x1),f(-x2)=-f(x2),
即有-f(x1)>-f(x2),即f(x1)<f(x2),
则函数f(x)在(-∞,0]上单调递增;
(2)由(1)可得,f(x)在R上单调递增,
不等式f(2x-1)<f($\frac{1}{3}$)即为
2x-1<$\frac{1}{3}$,解得x<$\frac{2}{3}$.
故所求x的范围是(-∞,$\frac{2}{3}$).
点评 本题考查函数的单调性和奇偶性的判断和运用:解不等式,考查运算能力,属于中档题.

练习册系列答案
相关题目
8.腾冲第八中学数学组有实习老师共5名,现将他们分配到高二年级的90、91、92三个班实习,每班至少1名,最多2名,则不同的分配方案有( )
| A. | 30种 | B. | 90种 | C. | 180种 | D. | 270种 |
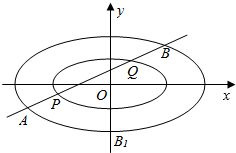 已知椭圆C1,$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>1)与椭圆C2:$\frac{{x}^{2}}{4}$+y2=1有相同的离心率,经过点P(-2,0)的直线l与椭圆C2相交于P、Q两点,与椭圆C1相交于A、B两点.
已知椭圆C1,$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>1)与椭圆C2:$\frac{{x}^{2}}{4}$+y2=1有相同的离心率,经过点P(-2,0)的直线l与椭圆C2相交于P、Q两点,与椭圆C1相交于A、B两点.