题目内容
(5分)(2011•广东)设函数f(x)=x3cosx+1,若f(a)=11,则f(﹣a)= .
﹣9
试题分析:由于函数f(x)=x3cosx+1,是一个非奇非偶函数,故无法直接应用函数奇偶性的性质进行解答,故可构造函数g(x)=f(x)﹣1=x3cosx,然后利用g(x)为奇函数,进行解答.
解:令g(x)=f(x)﹣1=x3cosx
则g(x)为奇函数,
又∵f(a)=11,
∴g(a)=f(a)﹣1=11﹣1=10
∴g(﹣a)=﹣10=f(﹣a)﹣1
∴f(﹣a)=﹣9
故答案为:﹣9
点评:本题考查的知识点是函数奇偶性的性质,其中构造出奇函数g(x)=f(x)﹣1=x3cosx,是解答本题的关键.

练习册系列答案
相关题目
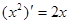 ,
,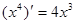 ,
,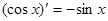 ,由归纳推理可得:若定义在
,由归纳推理可得:若定义在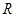 上的函数
上的函数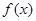 满足
满足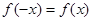 ,记
,记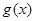 为
为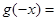 ( )
( )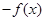
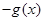
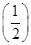 x,则f(1),g(0),g(-1)之间的大小关系是______________.
x,则f(1),g(0),g(-1)之间的大小关系是______________. 为奇函数,则a+b=________.
为奇函数,则a+b=________.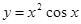 部分图象可以为( )
部分图象可以为( )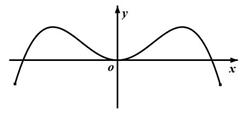
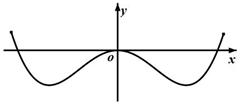
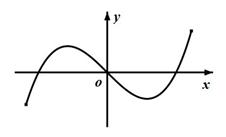
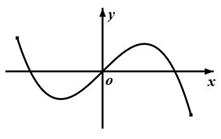
 上的奇函数
上的奇函数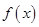 ,
,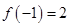 ,且当
,且当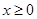 时,
时, 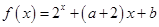 (
(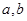 为常数),则
为常数),则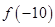 的值为 .
的值为 .