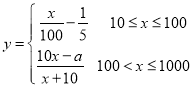题目内容
【题目】已知函数![]() ,
,![]() .
.
(1)当![]() ,
,![]() 时,求函数
时,求函数![]() 在
在![]() 处的切线方程,并求函数
处的切线方程,并求函数![]() 的最大值;
的最大值;
(2)若函数![]() 的两个零点分别为
的两个零点分别为![]() ,
,![]() ,且
,且![]() ,求证:
,求证:![]() .
.
【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】
(1)当![]() 时,求得斜率和切点的坐标,利用点斜式写出切线方程.根据函数的导数求得函数的单调区间,由此求得函数的最大值.(2)将两个零点代入函数
时,求得斜率和切点的坐标,利用点斜式写出切线方程.根据函数的导数求得函数的单调区间,由此求得函数的最大值.(2)将两个零点代入函数![]() 的解析式,将得到两个方程相减,化简为
的解析式,将得到两个方程相减,化简为![]() 的表达式,通过令
的表达式,通过令![]() ,将所要证明的不等式转化为证明
,将所要证明的不等式转化为证明![]() ,构造函数
,构造函数![]() ,利用导数证明
,利用导数证明![]() ,由此证得原不等式成立.
,由此证得原不等式成立.
(1)解:当![]() ,
,![]() 时,
时,![]() ,
,![]() ,
,
则![]() ,切点为
,切点为![]() ,故函数
,故函数![]() 在
在![]() 处的切线方程为
处的切线方程为![]() .
.
令![]() ,则
,则![]() 在
在![]() 是减函数,
是减函数,
又![]() ,∴
,∴![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() 在
在![]() 上是增函数,在
上是增函数,在![]() 是减函数,
是减函数,![]() .
.
(2)证明:∵![]() ,
,![]() 是
是![]() 的两个零点,不妨设
的两个零点,不妨设![]() ,
,
∴![]() ,
,
![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
相减得:![]()
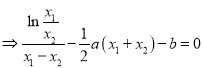
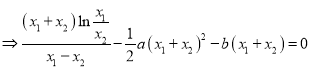 ,
,
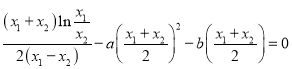 ,
,
∴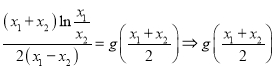
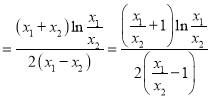 ,
,
令![]() ,即证
,即证![]() ,
,![]() ,
,
![]() ,
,
令![]() ,
,![]() ,
,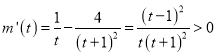 ,
,
![]() 在
在![]() 上是增函数,又∵
上是增函数,又∵![]() ,
,
∴![]() ,
,![]() ,命题得证.
,命题得证.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目