题目内容
已知矩阵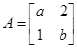 有一个属于特征值
有一个属于特征值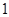 的特征向量
的特征向量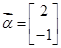 ,
,
①求矩阵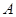 ;
;
②已知矩阵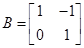 ,点
,点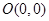 ,
,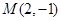 ,
,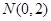 ,求
,求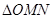 在矩阵
在矩阵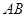 的对应变换作用下所得到的
的对应变换作用下所得到的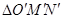 的面积.
的面积.
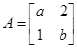 有一个属于特征值
有一个属于特征值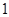 的特征向量
的特征向量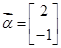 ,
,①求矩阵
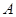 ;
;②已知矩阵
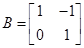 ,点
,点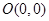 ,
,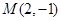 ,
,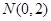 ,求
,求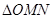 在矩阵
在矩阵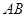 的对应变换作用下所得到的
的对应变换作用下所得到的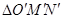 的面积.
的面积.① ②
②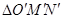 的面积为
的面积为
 ②
②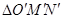 的面积为
的面积为
试题分析:①根据矩阵
 有一个属于特征值1的特征向量
有一个属于特征值1的特征向量 可得
可得

 ,从而可求矩阵
,从而可求矩阵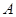 ;
;②先计算
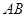 ,从而可得点
,从而可得点 变成点
变成点 即可计算
即可计算 的面积.
的面积.试题解析:①由已知得:


 ,
,∴
 解得
解得 故
故 .
. ②∵



∴


 ,
,

 ,
,


即点
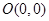 ,
,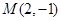 ,
,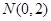 变成点
变成点 ,
, ,
,
∴
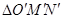 的面积为
的面积为

练习册系列答案
相关题目
 所对应的变换
所对应的变换 把直线
把直线 变换为自身,求实数
变换为自身,求实数 ,并求
,并求 的逆矩阵.
的逆矩阵.
 在矩阵C对应的变换作用下的曲线方程.
在矩阵C对应的变换作用下的曲线方程. ,点
,点 在变换
在变换 下变换为点
下变换为点 ,则
,则