题目内容
在四边形ABCD中,A、B为定点,C、D是动点,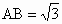 ,BC=CD=AD=1,△ABD与△BCD的面积分别为S与T.
,BC=CD=AD=1,△ABD与△BCD的面积分别为S与T.
(1)求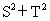 的取值范围;
的取值范围;
(2)当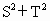 取得最大值时,求∠BCD的值.
取得最大值时,求∠BCD的值.
答案:略
解析:
提示:
解析:
|
解:(1)如图所示,设BD=2x, 则 ∴ 在△CDB中,过C作CE⊥BD交BD于E, ∵CD=CB=1, ∴DE=BE=x. ∴ 从而 又
∴ ∴当 ∵ ∴ 即 (2) 此时∠BCD=120°. |
提示:
|
设BD=2x,利用正弦定理和余弦定理将 形式求最值.求最值时注意x的取值范围. |

练习册系列答案
相关题目

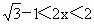 ,
,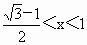 .
.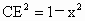 .
.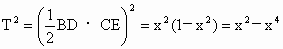 .
.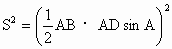
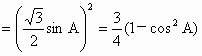
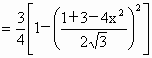
 .
.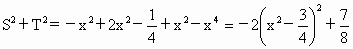 .
.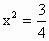 时,
时,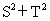 取得最大值为
取得最大值为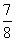 .
.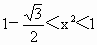 ,
,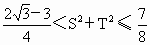 .
.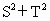 的取值范围是
的取值范围是 .
.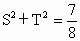 时,
时,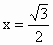 ,
,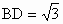 ,
, 如图所示,在四边形ABCD中,EF∥BC,FG∥AD,则
如图所示,在四边形ABCD中,EF∥BC,FG∥AD,则