题目内容
已知双曲线的方程为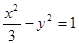 ,则此双曲线的焦点到渐近线的距离为
,则此双曲线的焦点到渐近线的距离为
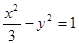 ,则此双曲线的焦点到渐近线的距离为
,则此双曲线的焦点到渐近线的距离为 1
试题分析:根据题意,由于双曲线的方程为
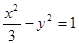 ,可知
,可知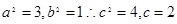 ,则可知焦点在x轴上,渐近线方程为y=
,则可知焦点在x轴上,渐近线方程为y=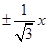 ,那么化为一般式,结合点到直线的距离公式可知d
,那么化为一般式,结合点到直线的距离公式可知d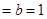 ,g故答案为1.
,g故答案为1.点评:解决的关键是熟悉双曲线中a,bc表示其渐近线方程以及点到直线的距离公式的运用,属于基础题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
题目内容
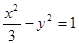 ,则此双曲线的焦点到渐近线的距离为
,则此双曲线的焦点到渐近线的距离为 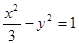 ,可知
,可知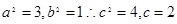 ,则可知焦点在x轴上,渐近线方程为y=
,则可知焦点在x轴上,渐近线方程为y=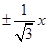 ,那么化为一般式,结合点到直线的距离公式可知d
,那么化为一般式,结合点到直线的距离公式可知d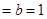 ,g故答案为1.
,g故答案为1.
 阅读快车系列答案
阅读快车系列答案